Question

A circus is to be erected in the form of a cone surmounted on a cylinder. The total height of the tent is $49m$. Diameter of the base is $42m$ and the height of the cylinder is $21m$. Find the cost of canvas needed to make the tent, if the cost of canvas is ${\text{Rs}}{\text{. 12}}{\text{.50/}}{{\text{m}}^2}$. (Take $\pi = \dfrac{{22}}{7}$)

Answer 1

Hint: We will draw the schematic diagram and then, from the figure, we can say that the cost of canvas can be found if we multiply the cost of canvas per ${m^2}$ with the total surface area of the tent. And the total surface area of the tent will be equal to the sum of the individual curved surface areas of the cone and the cylinder. The curved surface area (CSA) of the cone is $\pi rl$, where r is the radius of the base of the cone and l is the slant height of the cone. The CSA of the cylinder is $2\pi rh$, where r is the radius of the base of the cylinder and h is the height of the cylinder.

Complete step-by-step answer:
We are given that a circus is to be erected where a cone is surmounted on a cylinder. The total height of the tent is $49m$ and the diameter of base of the cylinder is $42m$ with height $21m$.
We are required to calculate the cost of canvas needed to make the tent given that the cost of canvas is ${\text{Rs}}{\text{. 12}}{\text{.50/}}{{\text{m}}^2}$.
The figure will be:

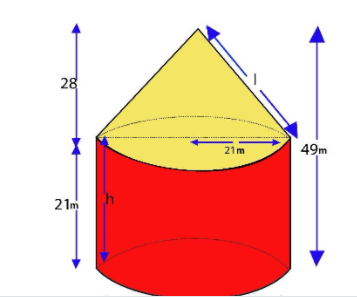
From the figure, we can say that the total cost needed for the canvas will be equal to the cost of the canvas per ${m^2}$ multiplied with the total surface area of the tent i.e., the total cost of the tent = ${\text{Rs}}{\text{. 12}}{\text{.50/}}{{\text{m}}^2}$$ \times $ total surface area of the tent.
Since the tent comprises a cone and a cylinder, the total surface area of the tent will be equal to the sum of the individual curved surface areas of the cone and the cylinder i.e., the total surface area of the tent = CSA of cone + CSA of cylinder.
The curved surface area of the cylinder is given by the formula: $2\pi rh$, where r is the radius of the base of the cylinder and h is the height of the cylinder.
We have the height of the cylinder as $21m$ and the radius of the cylinder = $\dfrac{{{\text{diameter of cylinder}}}}{2} = \dfrac{{42}}{2} = 21m$.
The curved surface area of the cone is given by the formula: $\pi rl$, where r is the radius of the base of the cone and l is the slant height of the cone.
We know that the base of the cone and the top of the cylinder overlaps and hence the radius of the cylinder will be equal to the radius of the cone i.e., radius of the cone = $21m$
Now, the total height of the tent is $49m$ and the height of the cylindrical portion is $21m$, therefore, the height of the cone will be: $49m - 21m = 28m$. We have to use the slant height of the cone which is given by the formula: $l = \sqrt {{r^2} + {h^2}} $, where r is the radius and h is the height of the cone.
$ \Rightarrow l = \sqrt {{{\left( {21} \right)}^2} + {{\left( {28} \right)}^2}} $
$ \Rightarrow l = \sqrt {441 + 784} = \sqrt {1225} = 35$
So, the total surface area of the tent = $2\pi rh + \pi rl$. On putting values of the respective radii, the height and the slant height, we get
$ \Rightarrow $ TSA of the tent = $\left( {2 \times \dfrac{{22}}{7} \times 21 \times 21} \right) + \left( {\dfrac{{22}}{7} \times 21 \times 35} \right)$
$ \Rightarrow $ TSA of the tent = $2772 + 2310$
$ \Rightarrow $ TSA of the tent =$5082{m^2}$
Therefore, the total surface area of the tent is $5082{m^2}$. So, if the cost per ${m^2}$ is ${\text{Rs}}{\text{. 12}}{\text{.50}}$, then the cost for $5082{m^2}$ will be equal to the product of the area and the cost per ${m^2}$.
$ \Rightarrow $ The total cost of the canvas = ${\text{Rs}}{\text{. }}12.50/{m^2} \times 5082{m^2}$
$ \Rightarrow $ The total cost of the canvas = ${\text{Rs}}{\text{. 63,525}}$
Hence, the total cost of the canvas needed for the tent is ${\text{Rs}}{\text{. 63,525}}$.

Note: In this question, you may think why we have represented the total surface area of the tent as an individual sum of the curved surface areas. It is so because the tent comprises a cone which is surmounted on a cylinder and the canvas can only be wrapped outside of the figure and that’s why we have not used the individual total surface area of the cone or cylinder. You should also take care of the difference between the slant height and the height of the cone.