Question

A charge of one coulomb is located in the center of a sphere of radius $10\,cm$ and the cube of side $20\,cm$. The ratio of flux from sphere and cube will be?
A. More than one
B. Less than one
C. One
D. None of these

Answer 1

Hint: To answer this question we will first know about gauss law as it is the basis to this question. Using the gauss law which states the relation between charge enclosed in a surface and electric flux, we will find individual values of flux through cube and sphere separately and then find its ratio to get the answer.

Formula used:
\[\phi = \dfrac{Q}{{{\varepsilon _0}}}\]
Where, \[\phi \] is the electric flux, \[Q\]- is a charged enclosed Gaussian surface and \[{\varepsilon _0}\]- is the permittivity of free space.

Complete step by step answer:
Let us look at the gauss law for electrostatics: The static electric field created by a distribution of electric charges is described by Gauss's law for the electric field. It claims that the total electric charge enclosed by any closed surface is proportional to the electric flux through that surface. let us now look at the question: Look at the following image :

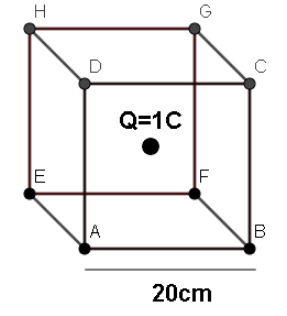
In the case of a cube of 20cm. a charge of 1C is placed inside it. the flux in this case will be given by :
\[{\phi _1} = \dfrac{Q}{{{\varepsilon _0}}}\]
\[\Rightarrow {\phi _1} = \dfrac{1}{{{\varepsilon _0}}}......(1)\]
Now let's look at the sphere with a charge of 1C enclosed in it. Look at the figure below:

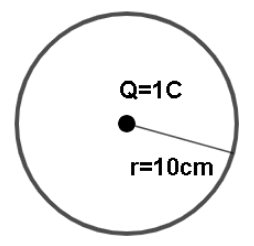
In the case of a sphere of radius 10cm, a charge of 1C is placed inside it. the flux in this case will be given by :
\[{\phi _2} = \dfrac{Q}{{{\varepsilon _0}}}\]
\[\Rightarrow {\phi _2} = \dfrac{1}{{{\varepsilon _0}}}.....(2)\]
Now we are suppose to find the ratio between flux produced by sphere and cube. Hence we have to find \[\dfrac{{{\phi _2}}}{{{\phi _1}}}\].
\[\dfrac{{{\phi _2}}}{{{\phi _1}}} = \dfrac{{\dfrac{1}{{{\varepsilon _0}}}}}{{\dfrac{1}{{{\varepsilon _0}}}}}\]
\[\therefore \dfrac{{{\phi _2}}}{{{\phi _1}}} = 1\].

Hence the correct option is C.

Note: We can also give an answer to this question in a very simple way, we know that flux is \[\dfrac{1}{{{\varepsilon _0}}}\] the total charge in it. and here both the cube and sphere act as a Gaussian surface. And the charge enclosed in both the Gaussian surfaces is the same. Hence it is obvious that the flux through them will be the same. And if the flux in both sphere and cube is the same, then their ratio will be 1.