Question

A carpenter has constructed a toy as shown in the figure If the density of the material of the sphere is 12 times that of cone, the position of the centre of mass the toy is given by

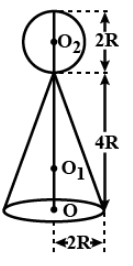
A. At a distance of 2 R from O
B. At a distance of 3 R from O
C. At a distance of 4 R from O
D. At a distance of 5 R from O

Answer 1

Hint: The term "density" refers to the amount of mass per unit of volume. An object's average density is proportional to its total mass divided by its total volume. An object composed of a more dense material (such as iron) would have less volume than one made of a less dense substance of comparable mass (such as water).

Complete step by step answer:
The centre of mass of a mass distribution in space (also known as the equilibrium point) is the special point in physics where the weighted relative location of the distributed mass amounts to zero. A force may be applied to this point to induce a linear acceleration without causing an angular acceleration.

We know that
$\text{Mass} = \dfrac{\text{Density}}{\text{Volume}}$
If the density of cone is$\rho $, then mass of cone = $ = {\text{ density }} \times {\text{ volume }} = \dfrac{{\rho 1}}{{3\pi {{(2{\text{R}})}^2}}}$
i.e, ${m_1} = \dfrac{{16}}{{3\pi {{({\text{R}})}^3}\rho }}$
Hence, This mass is concentrated at a height from
${\text{O}} = \dfrac{h}{4} = \dfrac{{4R}}{h}$
From the above calculations
$\text{Mass of sphere} = {m_2} \\
\Rightarrow \text{Mass of sphere} = {\text{ density }} \times {\text{ volume }} \\
\Rightarrow \text{Mass of sphere} = \dfrac{{12\rho 4}}{{3\pi {{({\text{R}})}^3}}} \\
\Rightarrow \text{Mass of sphere} = 16\pi {{\text{R}}^3}\rho $

This mass is actually concentrated at ${O_2}$, i.e. at a distance of \[4R + R = 5R\] from O.Hence centre of mass of whole system will be
${{\text{Y}}_{{\text{cm}}}} = \dfrac{{{{\text{m}}_1}{{\text{y}}_1} + {{\text{m}}_2}{{\text{y}}_2}}}{{\;{{\text{m}}_1} + {{\text{m}}_2}}} \\$
Here ${y_1} = R{\text{ and }}{y_2} = 5R$
${Y_{cm}} = \dfrac{{mR + 3m(5R)}}{{m + 3m}} \\$
$\Rightarrow {Y_{cm}} = \dfrac{{16{\text{mR}}}}{{4\;{\text{m}}}} \\ $
$\therefore {Y_{cm}} = 4R$

Hence option C is correct.

Note: When formulated with respect to the centre of mass, physics calculations are sometimes simplified. It is a fictional point at which an object's entire mass can be believed to be condensed in order to visualise its motion. To put it another way, the centre of mass is the particle counterpart to a given object when Newton's laws of motion are applied.