
A car petrol tank is $\dfrac{3}{8}$ full. After that, the petrol tank is filled with 30 litres of petrol and the tank is full. What is the capacity of the tank?
(a) 30 litres
(b) 36 litres
(c) 42 litres
(d) 48 litres
Answer
597.6k+ views
Hint: Let us assume that the capacity of the tank is x. A car petrol tank is $\dfrac{3}{8}$ full it means the volume occupied by the petrol in the tank is $\dfrac{3}{8}x$. Now, we added 30 litres of the petrol that make the petrol tank full so the addition of $\dfrac{3}{8}x$ and 30 litres is equal to the total capacity of the tank i.e. x. Solving this equation will give us the value of x.
Complete step-by-step answer:
Let us assume that the capacity of the petrol tank is “x”.
The volume of petrol tank when the car tank is $\dfrac{3}{8}$ full is the multiplication of $\dfrac{3}{8}$ by x which is equal to:
$\dfrac{3}{8}\left( x \right)$
Now, 30 litres of the petrol is added to the tank which makes the total volume of the petrol equal to the capacity of the petrol tank. Adding 30 litres to $\dfrac{3}{8}\left( x \right)$ we get,
$30+\dfrac{3}{8}x$
Equating the above volume to the total capacity of the tank i.e. x we get,
$30+\dfrac{3}{8}x=x$
Subtracting $\dfrac{3}{8}x$ on both the sides of the above equation we get,
$30=x-\dfrac{3}{8}x$
Taking 8 as L.C.M in the denominator on the right hand side of the above equation we get,
$\begin{align}
& 30=\dfrac{8x-3x}{8} \\
& \Rightarrow 30=\dfrac{5x}{8} \\
\end{align}$
On cross multiplying the above equation we get,
$240=5x$
Dividing 5 on both the sides of the above equation we get,
$\begin{align}
& \dfrac{240}{5}=x \\
& \Rightarrow 48=x \\
\end{align}$
From the above calculation, the value of x is equal to 48 and we have assumed above that the total capacity of the tank is x so the total capacity of the tank is 48 litres.
Hence, the correct option is (d).
Note: We have given in the question that “A car petrol tank is $\dfrac{3}{8}$ full”. This statement means that the volume of the tank filled with petrol is $\dfrac{3}{8}x$ not subtraction of $\dfrac{3}{8}x$ from x. You might have written the volume of the filled tank as $x-\dfrac{3}{8}x$. This is the wrong volume because this is the empty volume in the petrol tank which is not filled with petrol not the volume of petrol in the petrol tank.
In the below diagram, we have shown the petrol tank in which $\dfrac{3}{8}x$ represents EB and the empty space in the tank is AE.
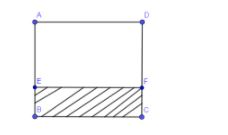
Complete step-by-step answer:
Let us assume that the capacity of the petrol tank is “x”.
The volume of petrol tank when the car tank is $\dfrac{3}{8}$ full is the multiplication of $\dfrac{3}{8}$ by x which is equal to:
$\dfrac{3}{8}\left( x \right)$
Now, 30 litres of the petrol is added to the tank which makes the total volume of the petrol equal to the capacity of the petrol tank. Adding 30 litres to $\dfrac{3}{8}\left( x \right)$ we get,
$30+\dfrac{3}{8}x$
Equating the above volume to the total capacity of the tank i.e. x we get,
$30+\dfrac{3}{8}x=x$
Subtracting $\dfrac{3}{8}x$ on both the sides of the above equation we get,
$30=x-\dfrac{3}{8}x$
Taking 8 as L.C.M in the denominator on the right hand side of the above equation we get,
$\begin{align}
& 30=\dfrac{8x-3x}{8} \\
& \Rightarrow 30=\dfrac{5x}{8} \\
\end{align}$
On cross multiplying the above equation we get,
$240=5x$
Dividing 5 on both the sides of the above equation we get,
$\begin{align}
& \dfrac{240}{5}=x \\
& \Rightarrow 48=x \\
\end{align}$
From the above calculation, the value of x is equal to 48 and we have assumed above that the total capacity of the tank is x so the total capacity of the tank is 48 litres.
Hence, the correct option is (d).
Note: We have given in the question that “A car petrol tank is $\dfrac{3}{8}$ full”. This statement means that the volume of the tank filled with petrol is $\dfrac{3}{8}x$ not subtraction of $\dfrac{3}{8}x$ from x. You might have written the volume of the filled tank as $x-\dfrac{3}{8}x$. This is the wrong volume because this is the empty volume in the petrol tank which is not filled with petrol not the volume of petrol in the petrol tank.
In the below diagram, we have shown the petrol tank in which $\dfrac{3}{8}x$ represents EB and the empty space in the tank is AE.

Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




