Question

A car moves towards north at a speed of $54Km{h^{ - 1}}$ for $1h.$ Then it moves eastward with the same speed for the same duration. The average speed and velocity of car for the complete journey is
(A) $54Km{h^{ - 1}},0$
(B) $15m{\sec ^{ - 1}},\dfrac{{15}}{{\sqrt 2 }}m{\sec ^{ - 1}}$
(C) $0,0$
(D) $0,\dfrac{{54}}{{\sqrt 2 }}km{h^{ - 1}}$

Answer 1

Hint: In Kinematics, average speed of a body is defined as total distance covered by the body in total time taken, whereas velocity of a body is defined as the speed of the body for a given displacement in a given time in a particular direction is called velocity of the body.

Complete step-by-step solution:
Let us suppose car moves from point O to point A in north direction with a speed of $54Km{h^{ - 1}}$ for $1h.$ and then moves with same speed for same duration in direction eastward from point A to point B. let us draw this diagram:

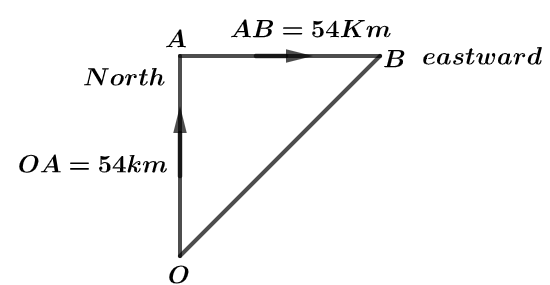
So, in order to calculate average velocity we know,
Total time taken to cover distance $OA + AB = 108Km$ is $2hours$ .
Hence, $average$ $speed = \dfrac{{OA + AB}}{2}$ .
$average$ $speed = \dfrac{{108}}{2}$ .
$average$ $speed = 54Km{h^{ - 1}}$ .
We will convert kilometre hour into meter per second as: $54Km{h^{ - 1}} = 54 \times \dfrac{5}{{18}}m{\sec ^{ - 1}}$
$54k{m^{ - 1}} = 15m{\sec ^{ - 1}}$
So, Average speed of the car is $15m{\sec ^{ - 1}}$ .
In order to calculate velocity of car, the displacement of the car is represented between point O and point B and hence, from Pythagoras theorem in diagram
$OB = \sqrt {2{{(54)}^2}} $
$OB = 54\sqrt 2 $
So, velocity is $Velocity = \dfrac{{OB}}{2}$
$Velocity = \dfrac{{54\sqrt 2 }}{2}$
$Velocity = \dfrac{{54}}{{\sqrt 2 }}Km{h^{ - 1}}$
Or
$Velocity = \dfrac{{15}}{{\sqrt 2 }}m{\sec ^{ - 1}}$
Hence, the correct option is (B) $15m{\sec ^{ - 1}}$ , $\dfrac{{15}}{{\sqrt 2 }}m{\sec ^{ - 1}}$

Note: We must remember that average speed is a scalar quantity and velocity is a vector quantity and in above problem velocity is in the direction of Point O to Point B. and the basic conversion of Kilometre per hour into meter per second is given as $1Km{h^{ - 1}} = \dfrac{5}{{18}}m{\sec ^{ - 1}}$ where $1Km = 1000m$ and $1hour = 3600\sec $ .