Question

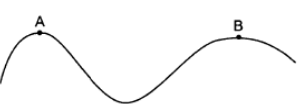
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car is ${N_A}\& {N_B}$ when it is the points $A$ and $B$ respectively.Information to decide the relation of ${N_A}\& {N_B}$

A. ${N_A} = {N_B}$
B. ${N_A} > {N_B}$
C. ${N_A} < {N_B}$
D. Insufficient data to determine the relation between ${N_A}\& {N_B}$.

Answer 1

Hint: The term "speed" is described as the pace at which an object's orientation changes in some direction. Speed is defined as the ratio of distance travelled to the time it took to travel that distance. Since speed has just one direction and no amplitude, it is a scalar quantity.

Complete step by step answer:
Constant speed, also known as uniform velocity, refers to something travelling at a constant and consistent speed or at an average speed. The product of the displacement of the object (on which the force is applied) and the part of the constant force that is parallel to the direction of displacement is the work performed by a constant force.

All points $A$ and $B$ are on the crests of the bends, with the car's mass 'mg' perpendicular to the ground. However, owing to the car's displacement on the curve, it will experience a weight reduction of $\dfrac{{m{v^2}}}{r}$, where 'v' is the car's constant speed and 'r' is the curve's radius. Since the numerator is constant, this weight loss is clearly inversely proportional to 'r.' The term $\dfrac{{m{v^2}}}{r}$ gets bigger as the 'r' gets smaller. Since 'r' at point $A$ is smaller than at point $B$, weight loss would be greater at $A$ than at $B$. It means that the apparent weight at $A$ is lower than at $B$.

${{\mathbf{N}}_{\text{A}}} = {\mathbf{mg}} - \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_{\text{A}}}}}$
${{\mathbf{N}}_B} = {\mathbf{mg}} - \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_B}}}$
Now, ${{\mathbf{r}}_{\mathbf{A}}} < {{\mathbf{r}}_{\mathbf{B}}}$
Hence, $\dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_{\text{A}}}}} > \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_{\text{B}}}}}$
So, $mg - \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_{\text{A}}}}} < \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{{\text{r}}_{\text{B}}}}}{\text{mg}}$
Hence, ${{\mathbf{N}}_{\mathbf{A}}} < {{\mathbf{N}}_{\mathbf{B}}}$

Hence, the correct answer is option C.

Note: The normal force is the aspect of a contact force that is perpendicular to the object's contact surface in mechanics. Standard is used in this context to mean perpendicular in a geometric sense, as opposed to the traditional use of normal to mean "regular" or "anticipated" in everyday language. Gravity acts on a human standing still on a plateau, pulling them down towards the Earth's centre until there is a countervailing force from the opposition of the platform's molecules, known as the "normal force."