Question

A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine is needed to fill the capsule?

Answer 1

Hint: The amount of medicine that can be held in the capsule depends upon the capacity that the capsule possesses . As capacity is equal to the volume, we are required to find the volume of the spherical capsule. Use:
${\text{Volume of sphere}} = \dfrac{4}{3}\pi {r^3}$

Complete step-by-step answer:

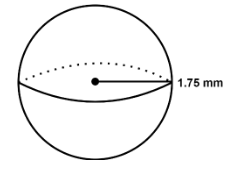
Diameter of capsule = 3.5 mm
Radius (r) =$\dfrac{{3.5}}{2} = 1.75mm$ $\left( {{\text{As radius = }}\dfrac{{{\text{Diameter}}}}{2}} \right)$
We know,
Medicine required = volume of capsule
And,
${\text{Volume of capsule}} = \dfrac{4}{3}\pi {r^3}$ (As it is spherical in shape given)
Substituting the value of r, we get
$\dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {(1.75)^3}m{m^3}$
\[ = \dfrac{4}{3} \times \dfrac{{22}}{7} \times 1.75 \times 1.75 \times 1.75m{m^3}\]
\[ = \dfrac{4}{3} \times \dfrac{{22}}{7} \times \dfrac{{175}}{{100}} \times \dfrac{{175}}{{100}} \times \dfrac{{175}}{{100}}m{m^3}\]
(Removing decimals for easier calculation)
= 471625/2100
=22.458
⟹ Therefore, 22.458 $mm^3$ volume of medicine is required to fill the capsule.

Note: Check carefully the amount of medicine to be filled (full or half the capsule) as given in the question and then proceed accordingly.
Always complete the answer with respective units asked / given in the question.