Question

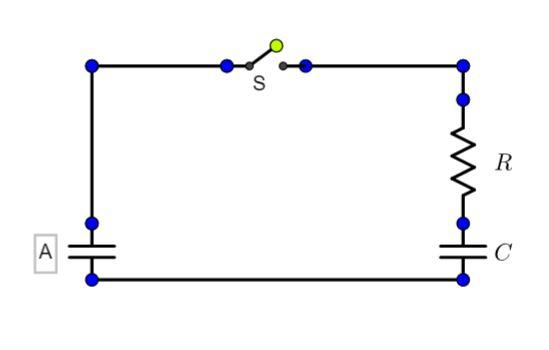
A capacitor of capacitance ${{C}_{0}}$ is charged to a potential ${{V}_{0}}$ and is connected with another capacitor of capacitance $C$ as shown. After closing the switch $S$ , the common potential across the two capacitors becomes \[V\] . The capacitance $C$ is given by:
A. $\dfrac{{{C}_{0}}\left( {{V}_{0}}-V \right)}{{{V}_{0}}}$
B. $\dfrac{{{C}_{0}}\left( V-{{V}_{0}} \right)}{{{V}_{0}}}$
C. $\dfrac{{{C}_{0}}\left( V+{{V}_{0}} \right)}{{{V}_{0}}}$
D. $\dfrac{{{C}_{0}}\left( {{V}_{0}}-V \right)}{V}$

Answer 1

Hint: Calculate the initial charge stored in the capacitor, then calculate the final charge stored in the capacitor with potential $V$, we know all the charges in a system must be conserved and it cannot be dissipated.

Complete step-by-step answer:

Given,
The initial charge stored in the capacitor A is ${{C}_{0}}{{V}_{0}}$.
The final charge stored in the capacitor A when a potential $V$is introduced is ${{C}_{0}}V$

The final charge in the capacitor $C$ is $CV$

We know, total charge must be conserved,
$\therefore {{C}_{0}}{{V}_{0}}={{C}_{0}}V+CV$
$\Rightarrow C=\dfrac{{{C}_{0}}\left( {{V}_{0}}-V \right)}{V}$
The correct option is (D).

Additional Information:
Capacitance is the potential of a system to store an electric charge.
$q=CV$ is the formula for capacitance, where q is the charge, C is the capacitance and V is the potential or voltage.
A device that shows capacitance is known as capacitor.
Farads(F) is the unit of capacitance.
The law of conservation of energy states that the total energy of a system stays constant and it can never be changed without any external features.

Note: The capacitor A initially had charge ${{V}_{0}}$ , but when the circuit was closed, the common potential between the two capacitors became V. Thus we at first have to find the initial charge then the final charge and they are conserved.