Question

A capacitor of capacitance $1\mu F$ withstands the maximum voltage of 6 kV, while another capacitor of capacitance $2\mu F$ withstands the maximum voltage of 4 kV. If they are connected in series, the combination can withstand a maximum voltage of
A) 3 kV
B) 6 kV
C) 10 kV
D) 9 kV

Answer 1

Hint: The charge present on the respective capacitors can be calculated minimum out of which will be the maximum charge (as more charge than that will break the circuit). The maximum voltage can be calculated using this maximum charge and respective capacitances.

Formula to be used:
$C = \dfrac{q}{V}$ where,
C = Capacitance
q = Charge
V = Voltage
For conversions:
\[1\mu F = {10^{ - 6}}F\]
${\text{1 }}kV \to {10^3}V$

Complete step by step answer:
Given:
Capacitance capacitor of 1 $\left( {{C_1}} \right)$= \[1\mu F \to {10^{ - 6}}F\]
Maximum voltage capacitor 1 can withstand \[\left( {{V_1}} \right)\] = $6{\text{ }}kV \to 6 \times {10^3}V$
Capacitance capacitor of 2 $\left( {{C_2}} \right)$ = \[2\mu F \to 2 \times {10^{ - 6}}F\]
Maximum voltage capacitor 2 can withstand \[\left( {{V_2}} \right)\] = ${\text{4 }}kV \to 4 \times {10^3}V$
As, capacitance is defined as charge upon volume:
$C = \dfrac{q}{V}$ ___________ (1)
$q = CV$
The maximum value charge each capacitor can have can be given as:
For capacitor 1:
${q_1} = {C_1}{V_1}$
Substituting the values, we get:
$
  {q_1} = {10^{ - 6}} \times 6 \times {10^3} \\
  {q_1} = 6 \times {10^{ - 3}}C \\
 $
For capacitor 2:
${q_2} = {C_2}{V_2}$
Substituting the values, we get:
$
  {q_1} = 2 \times {10^{ - 6}} \times 4 \times {10^3} \\
  {q_1} = 8 \times {10^{ - 3}}C \\
 $
When we connect them in series, the circuit can be given as:

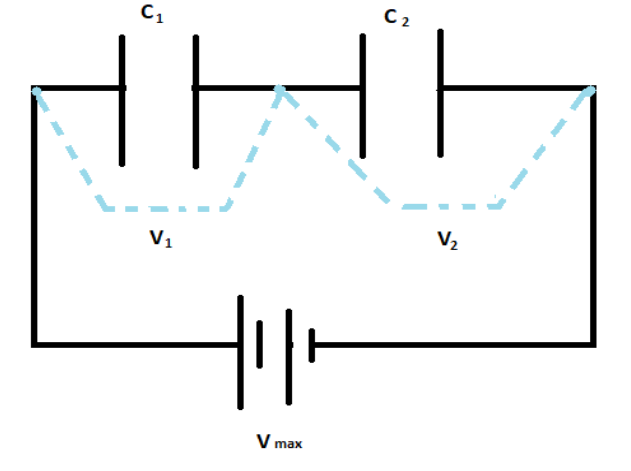
\[{V_1}\] and \[{V_2}\] are effective voltages across the capacitors and \[{V_{\max }}\] is the required maximum voltage which can be given as:
\[{V_{\max }} = {V_1} + {V_2}\] __________ (2)
Now, the maximum allowed on both the will be the minimum out of two because if the charge is more than that the circuit will break.

$
  {q_{\max }} = {q_1} = {q_2} \\
  {q_{\max }} = 6 \times {10^{ - 3}}C \\
 $
Using (1):
$C = \dfrac{q}{V}$
$V = \dfrac{q}{C}$
From (2):
\[{V_{\max }} = {V_1} + {V_2}\]
\[{V_{\max }} = \dfrac{{{q_1}}}{{{C_1}}} + \dfrac{{{q_2}}}{{{C_2}}}\]
Substituting the given values, we get:
\[{V_{\max }} = \dfrac{{6 \times {{10}^{ - 3}}}}{{{{10}^{ - 6}}}} + \dfrac{{6 \times {{10}^{ - 3}}}}{{2 \times {{10}^{ - 6}}}}\]

\[{V_{\max }} = 9 \times {10^3}\]
\[{V_{\max }} = 9kV\]
Therefore, if the given capacitors are connected in series, the combination can withstand a maximum voltage of 9 kV and hence the correct option D).

Note:SI units of various quantities are:
Capacitance (C) = Faraday (F)
Voltage (V) = Volts (V)
Charge (q) = Coulombs (C)
Capacitors are used to store energy as electric charge and hence are used for charging purposes.