Question

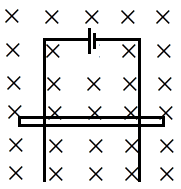
A capacitor of capacitance \[100\mu F\] is connected to a smooth railing and connector of mass 1 kg and length 1 m. Whole system is in a vertical plane and a magnetic field of strength $100T$ is applied perpendicular to the plane of circuit as shown Connector is released under gravity. The time (in sec) after which the dielectric of the capacitor will burn out is $k\times {{10}^{3}}$ then find the value of k. Breaking strength of dielectric is $5\times {{10}^{8}}V/m$. (d is the distance between plates of capacitor = 1mm)

Answer 1

Hint: We are given the capacitance, length and mass of the capacitor and the strength of the magnetic field in which the capacitor is placed. We can calculate the time taken to burn the capacitor from the given information. Then by comparing it with the given value of time, we will get the solution.

Formula used:
$C=\dfrac{Q}{V}$
$V=BvL$
$F=ma$

Complete step by step answer:
In the question we are given the capacitance of a capacitor as \[100\mu F\]and it is said that the capacitor is connected to a smooth railing of mass 1 kg and length 1 m.
The whole system is said to be in a vertical plane and the magnetic field applied perpendicular to the plane of circuit is given as $100T$.
We know that the capacitance of the capacitor can be given by the equation,
$C=\dfrac{Q}{V}$, where ‘C’ is the capacitance, ‘Q’ is the charge and ‘V’ is the potential.
Therefore we can write the potential from the above equation as,
$\Rightarrow V=\dfrac{Q}{C}$
We know that the potential in the magnetic field will be,
$V=BvL$, were ‘B’ is the magnetic field, ‘v’ is the velocity and ‘L’ is the length.
By equating these two equations for potential, we will get
$\Rightarrow \dfrac{Q}{C}=BvL$
$\Rightarrow Q=BvLC$
By taking the differential of above equation with respect to time we can write,
$\Rightarrow \dfrac{dQ}{dt}=\dfrac{d\left( BvLC \right)}{dt}$
Here we know that the magnetic field, capacitance and length are constants. We also know that the rate of change of charge with respect to time is current. Therefore we will get,
$\Rightarrow I=BCL\dfrac{dv}{dt}$, where ‘$I$’ is the current.
In the above equation, we know that the first derivative of velocity is acceleration. Thus,
$\Rightarrow I=BCLa$, were ‘a’ is the acceleration.
Now let us draw the free body diagram of the capacitor rod in the magnetic field.

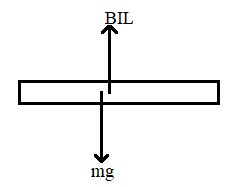
Here the two forces acting on the body are the force due to magnetic field,
$F=BIL$
And the force due to weight of the body,
$F=mg$
Since they are acting in the opposite direction, we will get the net force on the capacitor as,
$F=mg-BIL$
Now we know that force is generally given by the equation,
$F=ma$
By substituting for the force experienced here in the above equation we will get,
$\Rightarrow ma=mg=BIL$
From this we can write the acceleration as,
$\Rightarrow a=\dfrac{mg-BIL}{m}$
$\Rightarrow a=g-\dfrac{BIL}{m}$
$\Rightarrow a=g-\left( \dfrac{BL}{m} \right)I$
From earlier calculations we have, $I=BCLa$. Hence we can substitute this for the current in the above equation.
$\Rightarrow a=g-\left( \dfrac{BL}{m} \right)\left( BCLa \right)$
$\Rightarrow a=g-\left( \dfrac{{{B}^{2}}{{L}^{2}}Ca}{m} \right)$
$\Rightarrow g=a+\left( \dfrac{{{B}^{2}}{{L}^{2}}Ca}{m} \right)$
$\Rightarrow g=a\left( 1+\dfrac{{{B}^{2}}{{L}^{2}}C}{m} \right)$
$\Rightarrow g=a\left( \dfrac{m+{{B}^{2}}{{L}^{2}}C}{m} \right)$
$\Rightarrow a=\dfrac{g}{\left( \dfrac{m+{{B}^{2}}{{L}^{2}}C}{m} \right)}$
$\therefore a=\dfrac{mg}{m+{{B}^{2}}{{L}^{2}}C}$
Since acceleration, $a=\dfrac{dv}{dt}$ we can write the above equation as,
$\Rightarrow \dfrac{dv}{dt}=\dfrac{mg}{m+{{B}^{2}}{{L}^{2}}C}$
$\Rightarrow dv=\left( \dfrac{mg}{m+{{B}^{2}}{{L}^{2}}C} \right)\times dt$
By integrating this we will get the velocity as,
$\Rightarrow v=\left( \dfrac{mg}{m+{{B}^{2}}{{L}^{2}}C} \right)\times t$
This is the velocity for the dielectric of the capacitor to burn.
In the question we are given the breaking strength of the capacitor as $5\times {{10}^{8}}V/m$. That is,
$\dfrac{V}{d}=5\times {{10}^{8}}V/m$, were ‘d’ is the distance between the plates of the capacitor given as $1mm=1\times {{10}^{-3}}m$
Therefore,
$\Rightarrow V=5\times {{10}^{8}}\times d$
$\Rightarrow V=5\times {{10}^{8}}\times {{10}^{-3}}$
$\therefore V=5\times {{10}^{5}}$
We know that the potential is,
$V=BvL$
We have, $V=5\times {{10}^{5}}$, $B=100T$and $L=1m$. Therefore,
$\Rightarrow 5\times {{10}^{5}}=100\times 1\times v$
$\Rightarrow v=\dfrac{5\times {{10}^{5}}}{100\times 1}$
$\therefore v=5\times {{10}^{3}}$
Thus we get the velocity as $5\times {{10}^{3}}$.
From earlier calculation, we have the equation for velocity as,
$v=\left( \dfrac{mg}{m+{{B}^{2}}{{L}^{2}}C} \right)\times t$
Here we have,
$v=5\times {{10}^{3}}$
$m=1kg$
$g=10m/{{s}^{2}}$
$B=100T$
$L=1m$
$C=100\mu F={{10}^{-4}}F$
Therefore we can write,
$\Rightarrow 5\times {{10}^{3}}=\left( \dfrac{1\times 10}{1+\left( {{100}^{2}} \right)\left( {{1}^{2}} \right)\left( {{10}^{-4}} \right)} \right)t$
$\Rightarrow 5\times {{10}^{3}}=\left( \dfrac{1\times 10}{1+\left( {{100}^{2}} \right)\left( {{1}^{2}} \right)\left( {{10}^{-4}} \right)} \right)t$
$\Rightarrow 5\times {{10}^{3}}=\left( \dfrac{1\times 10}{1+\left( {{10}^{4}}\times {{10}^{-4}}\times 1 \right)} \right)t$
$\Rightarrow 5\times {{10}^{3}}=\left( \dfrac{10}{1+1} \right)t$
$\Rightarrow 5\times {{10}^{3}}=\left( \dfrac{10}{2} \right)t$
$\Rightarrow 5\times {{10}^{3}}=5t$
$\Rightarrow t=\dfrac{5\times {{10}^{3}}}{5}$
$\therefore t=1\times {{10}^{3}}$
This is the time after which the capacitor will burn. In the question this time is given as,
$t=k\times {{10}^{3}}$
By comparing these two equations, we get the value of k as 1, i.e
$k=1$

Note:
Parallel plate capacitors are formed when we arrange dielectric or any insulating material and electrodes. When we connect two parallel plates across a battery, the plates will get charged and an electric field will be formed between them. This setup is known as a parallel plate capacitor. We can only store a finite amount of energy in a parallel plate capacitor. If we store more energy, then the dielectric will burn.