Question

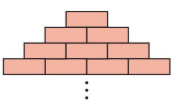
A bricklayer builds a triangular wall with layers of bricks as shown. If the bricklayer uses 171 bricks, how many layers did he build?

Answer 1

Hint: We can solve the given problem by using the concept of sum of the terms of arithmetic sequence. We have to use the formula \[s = \dfrac{n}{2}\left\{ {2a + (n - 1)d} \right\}\] and the ‘s‘ value is known to us as the bricklayer uses 171 bricks. So, we have to take ‘s’ as 171.

Complete step-by-step solution:
Given that the bricklayer uses 171 bricks, and we have to find the number of layers built that is taken as n so we have to find the value of n.
To solve this problem, we can use sum of arithmetic sequence the formula is given by
 \[s = \dfrac{n}{2}\left\{ {2a + (n - 1)d} \right\}\]
where
“S” is the sum of the arithmetic sequence,
“a” as the first term,
“d” the common difference between the terms,
“n” is the total number of terms in the sequence and
In this problem the value of a and d becomes 1 and we have to find the value of n so on substituting the values in the above formula we get
\[171 = \dfrac{n}{2}\left\{ {2(1) + (n - 1)(1)} \right\}\]
\[171 = \dfrac{n}{2}\left\{ {2 + n - 1} \right\}\]
\[171 = \dfrac{n}{2}\left\{ {1 + n} \right\}\]
On simplification we get
\[342 = {n^2} + n\]
It is a simple quadratic equation we can solve this by using factorization method first rearrange the terms in the above equation we can writ it as
\[{n^2} + n - 342 = 0\] now the factors for 342 is \[ + 19\] and \[ - 18\]
So, on simplification we get
\[{n^2} + 19n - 18n - 342 = 0\]
\[n(n + 19) - 18(n + 19) = 0\]
On simplification we get
\[n = - 19\] (or) \[n = 18\]
So, the number of layers build cannot be negative so \[n = 18\]
Therefore, the number of layers built is \[18\].

Note: In the above problem we have used the factorization method to solve the quadratic equation but we can also use the formula method to solve it. And we have used the formula \[s = \dfrac{n}{2}\left\{ {2a + (n - 1)d} \right\}\] we can also rewrite it as
\[s = \dfrac{n}{2}\left\{ {a + a + (n - 1)d} \right\}\]
\[ \Rightarrow s = \dfrac{n}{2}\left\{ {a + l} \right\}\]
where, \[l = a + (n - 1)d\] depending upon the requirement of the problem.