Question

A body of mass \[2Kg\] starts with an initial-velocity \[5\text{ }m/s\]. It the body is acted upon by a time dependent force \[\left( F \right)\] as shown in figure, then work done on the body in \[20s\] is

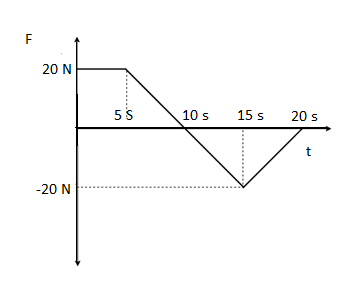
A. \[-875J\]
B. \[875J\]
C. \[600J\]
D. \[-600J\]

Answer 1

Hint: We have learnt the equation for work done by a force in terms of change in kinetic energy. To find the change in kinetic energy let’s analyze the graph.
Here the area under the graph gives impulse as the force is in the y coordinate and t is in the x coordinate. This Impulse of a body is related to change in momentum. Finding the momentum will lead us to work done.

Formula used:
\[Area,\text{ A=}\int{Fdt}=\text{Impulse}\]
\[W=\dfrac{1}{2}mv_{2}^{2}-\dfrac{1}{2}mv_{1}^{2}\]
\[\text{Impulse = m}{{\text{v}}_{2}}\text{- m}{{\text{v}}_{\text{1}}}\]
\[\text{Area of rectangle = h}\times \text{b}\]
\[\text{Area of right angled triangle =}\dfrac{1}{2}\times h\times b\]
\[\text{Area of triangle = }\dfrac{1}{2}\times \text{h}\times b\]

Complete answer:

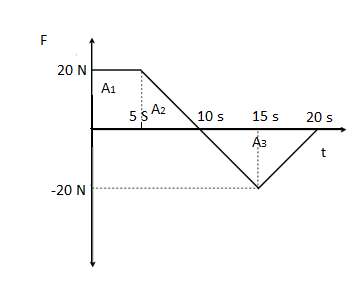
We have a force – time graph given. The area under force- time graph gives impulse.
\[Area,\text{ A=}\int{Fdt}=\text{Impulse}\]
Where,
\[\text{F = force acting on the object}\]
\[\text{dt = time interval}\]
To find impulse we need to find the area under the graph. Here area under the graph is algebraic sum of areas \[{{A}_{1}}\],\[{{A}_{2}}\] and \[{{A}_{3}}\]. Then,
\[\text{Area of }{{\text{A}}_{\text{1}}}\text{ }\!\!~\!\!\text{ = }\!\!~\!\!\text{ Area of rectangle = h}\times \text{b = 20 }\!\!\times\!\!\text{ 5 =100}\]
\[\text{Area of }{{\text{A}}_{2}}\text{ }\!\!~\!\!\text{ = }\!\!~\!\!\text{ Area of right angled triangle =}\dfrac{1}{2}\times h\times b\text{ =}\dfrac{\text{20 }\!\!\times\!\!\text{ 5}}{2}\text{=50}\]
\[\text{Area of }{{\text{A}}_{3}}\text{ }\!\!~\!\!\text{ = }\!\!~\!\!\text{ Area of triangle = }\dfrac{1}{2}\times \text{h}\times b\text{ =}\dfrac{\text{-20 }\!\!\times\!\!\text{ 10}}{2}\text{= -100}\]
Then,
\[\text{Impulse = 100 + 50 - 50 = }50Ns\]
We know,
\[\text{Impulse = Change in linear momentum}\]
Then,
\[\text{Impulse = m}{{\text{v}}_{2}}\text{- m}{{\text{v}}_{\text{1}}}\]
Where,
\[\text{m = mass of the object}\]
\[{{\text{v}}_{2}}\text{= final velocity}\]
\[{{\text{v}}_{1}}\text{= Initial velocity}\]
Given, \[mass,m=2Kg\]
\[\text{Impulse = 2}\left( {{\text{v}}_{2}}-{{\text{v}}_{1}} \right)\]
Here, \[{{v}_{1}}=5m/s\] and \[\text{Impulse=}50Ns\]
Then,
\[\text{50 = 2}\left( {{\text{v}}_{2}}-5 \right)\]
\[{{v}_{2}}=30m/s\]
Now,
\[\text{Work }\!\!~\!\!\text{ done on the body in 20s, W =Final Kinetic energy-Initial Kinetic energy}\]
\[W=\dfrac{1}{2}mv_{2}^{2}-\dfrac{1}{2}mv_{1}^{2}\] \[\left( \text{m is the mass of object} \right)\]
\[\text{W=}\dfrac{1}{2}\times 2\times {{\left( 30 \right)}^{2}}-\dfrac{1}{2}\times 2\times {{\left( 5 \right)}^{2}}\]
\[W=875J\]
Hence work done on the body in \[20s\] is, \[W=875J\]

So, the correct answer is “Option B”.

Note:
When finding the area under the graph, determine the shape of the graph first. Figure out what geometrical shape it is, and then by finding the area of that geometrical shape we could easily get the value of the desired quantity.
The area under the curve gives the magnitude of the quantity which is obtained by the product of the quantities signified by the x and y coordinates. To understand this better let’s consider a velocity-time graph. Let the y-axis represent the velocity of an object and let the x-axis represent the time taken by it. The area under the graph would denote the displacement of the object. We know that displacement is the product of velocity and time. Similarly, we can find velocity by finding the area under the acceleration-time graph. The impulse from the force-time graph can be found in the same way.