Question

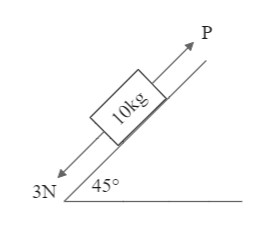
A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3N is applied on the block. The coefficient of static friction between the plane and the block is $0.6$. What should be the minimum value of force P, such that the block does not move downward? (Assume $g = 10m{s^{ - 2}}$)

A. 32N
B. 25N
C. 44N
D. 18N

Answer 1

Hint
The frictional force is exerted in the opposite direction of the motion of the object caused due to the gravitational force. For the block to not move forward (or backward), the forces acting on the block need to be balanced to equilibrium.
$\Rightarrow F = \mu N$, where F is the frictional force, $\mu $ is the coefficient of friction and N is the normal reaction.

Complete step by step answer
We have a block on the inclined plane, and are asked to find the force P for which the block remains in an equilibrium position. To attain this, the forces acting on the block in the horizontal and vertical direction alike need to be balanced. The data provided to us includes:
Mass of the block is 10 kg
Force applied on the block is 3 N
Gravitational acceleration $g = 10m{s^{ - 2}}$
Coefficient of friction $\mu = 0.6$
Inclined plane angle $\theta = 45$
For an inclined plane, we know that the components of mg will be acting vertically and horizontally on the block with respect to the inclined plane.
The normal reaction N exerted on the block will be equated by the vertical component of mg as:
$\Rightarrow N = mg\cos \theta $
Now in the horizontal direction, the force balance will be given as:
$\Rightarrow 3 + mg\sin \theta = F + P$ [Eq. 1]
F is the frictional force and it acts in the opposite direction of the force exerted on the block.
We know that the frictional force is given by:
$\Rightarrow F = \mu N = \mu mg\cos \theta $
Putting these values in the Eq. 1, gives us:
$\Rightarrow 3 + mg\sin \theta = \mu mg\cos \theta + P$
Solving for P, we get:
$\Rightarrow P = 3 + mg\sin \theta - \mu mg\cos \theta = 3 + mg(\sin \theta - \mu \cos \theta )$
Substituting the values:
$\Rightarrow P = 3 + 10 \times 10(\sin 45 - 0.6\cos 45)$
$\Rightarrow P = 3 + 100(\dfrac{1}{{\sqrt 2 }} - 0.6 \times \dfrac{1}{{\sqrt 2 }})$
This will give us the value of force P as:
$\Rightarrow P = 3 + 100\dfrac{1}{{\sqrt 2 }}(1 - 0.6) = 3 + \dfrac{{100 \times 0.4}}{{\sqrt 2 }}$
$\Rightarrow P = 3 + 28.3 = 31.3$
This is approximately equal to 32N. Hence, the correct answer is option (A).

Note
When inclined planes are considered, the force does not act in linear directions as it normally does. And as force is a vector quantity, the direction of actual application of force on the object determines the effects of it. For example, if the friction was absent here and we were to ignore the effect of the inclined plane, the value of P would be equal and opposite to 3N, and this would make us ignore the effect of gravity which is responsible for sliding the block down.