Question

A baseball diamond is a square with 90 foot sides. How far must the third baseman throw the ball to make it to the first base?

Answer 1

Hint: Now we are given with a square ground of 90 foot side. Now we know that the third baseman is diagonally opposite to first base. Hence we have the distance between third baseman and first base as the diagonal of the square. Now we will find the length of the diagonal by using Pythagora's theorem in right angle triangle ABC.

Complete step-by-step answer:
Now let us say the first base is point A. Now let us draw a square ABCD. Now we know that the third baseman is at point C.

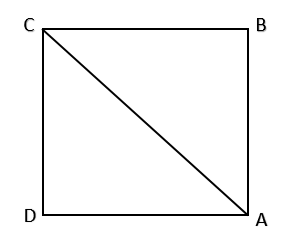
Now to make it to the first base the third baseman will throw the ball along AC.
Hence we want to find the distance if AC.
Now we know that ABCD is a square. Hence we have angle B is ${{90}^{\circ }}$
Now this means that triangle ABC is a right angle triangle.
Hence we can apply the Pythagoras theorem.
Now by Pythagoras theorem we have, $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$ .
Now since the sides of square are equal we have AB = BC.
Hence we get,
$\begin{align}
  & \Rightarrow A{{C}^{2}}=A{{B}^{2}}+A{{B}^{2}} \\
 & \Rightarrow A{{C}^{2}}=2A{{B}^{2}} \\
\end{align}$
Now substituting the value of side of square we get,
$\Rightarrow A{{C}^{2}}=2{{\left( 90 \right)}^{2}}$
Now taking square root in the above equation we get,
$\Rightarrow AC=90\sqrt{2}$
Hence the length of the diagonal is $90\sqrt{2}$ .
Hence the third baseman must throw the ball $90\sqrt{2}$ foot to reach the first baseman.

Note: Now note that we can directly solve the problem without using Pythagoras theorem. We know that for any square of length a the length of the diagonal is $\sqrt{2}a$ . Hence using this we can find the length of diagonal.