Question

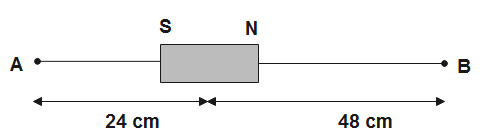
A bar magnet of length $3cm$ has points A and B along its axis at distances of $24cm$ and $48cm$ on the opposite sides. Ratio of magnetic fields at these points will be
(A). 8
(B). $\dfrac{1}{2\sqrt{2}}$
(C). 3
(D). 4

Answer 1

Hint: Figure shows a magnet with some magnetic pole strength. Two points are given along its axis at some distance from the poles. The magnetic field depends on the magnetic pole strength, absolute permittivity and the cube of distance from the center of magnet. Substituting the corresponding values we can calculate the magnetic field for each. The ratio is calculated by dividing both the fields.

Formula used:
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{r}^{3}}}$

Complete step by step solution:
The magnetic field strength determines the force acting on a magnet of unit pole strength due to the given magnet.
The magnetic field on the axis of a bar magnet is given by-
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{r}^{3}}}$ - (1)
Here, $B$ is the magnetic field
${{\mu }_{0}}$ is the absolute permittivity
$M$ is the magnetic pole strength
$r$ is the distance from the centre of them magnet along the axis
Given distance of point O from the center of magnet is $24cm$ and the distance of point B is $48cm$
From eq (1), the magnetic field at point A will be-
${{B}_{1}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{(24)}^{3}}}$ - (2)
From eq 92), the magnetic field at point b will be-
${{B}_{2}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{(48)}^{3}}}$ - (3)
Dividing eq (2) and eq (3), we get the ratio of both magnetic fields. Therefore,
$\begin{align}
  & \dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{(24)}^{3}}}}{\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{(48)}^{3}}}} \\
 & \Rightarrow \dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{{{(48)}^{3}}}{{{(24)}^{3}}} \\
 & \Rightarrow \dfrac{{{B}_{1}}}{{{B}_{2}}}=8 \\
\end{align}$
Therefore, the ratio of magnetic fields at point A and point B is 8. Hence, the correct option is (A).

Note: The magnetic pole strength of both north and south is the same as they are part of the same magnet. The dipole moment of a magnetic is the product of magnetic pole strength and the distance between the poles. The direction of dipole moment is from north to south.