Question

A, B, C and D are four points such that AB $ = m(2i - 6j + 2k), $ BC $ = i + 2j $ and
CD $ = n( - 6i + 15j - 3k) $ If AB and CD intersect at some point H, then
(This question has multiple correct options)
A. $ m \geqslant \dfrac{1}{2} $
B. $ n \geqslant \dfrac{1}{2} $
C.Area of $ \Delta BCH = \dfrac{1}{{2}}\sqrt 6 $
D.All of these

Answer 1

Hint: Here we will use the different concepts of the solutions of the equations, the cross-product of the vector equation and area of the triangle using the cross product of vectors. Substitute and simplify as per the required solution.

Complete step-by-step answer:

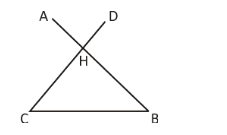
Given that lines AB and CD intersect at the point H and now connect the points C and B.
So, the triangle BCH is formed.
Also,
 $ \overrightarrow {AB} = m(2i - 6j + 2k), $
 $ \overrightarrow {BC} = i + 2j $ and
 $ \overrightarrow {CD} = n( - 6i + 15j - 3k). $
From the above figure, we can say that $ \overrightarrow {HB} = x\overrightarrow {AB} $
Where, “x” lies between zero and one. Such that $ 0 < x < 1 $
Similarly, $ \overrightarrow {CH} = y\overrightarrow {CD} $
Now, in $ \Delta CHB, $
 $ \Rightarrow \overrightarrow {CH} + \overrightarrow {HB} = \overrightarrow {CB} $
Place values from the given data –
 $ \Rightarrow yn( - 6i + 15j - 3k) + xm(2i - 6j + 2k) = - i - 2j $
Multiply the factors inside the bracket and simplify the above equations –
 $ \Rightarrow ( - 6yni + 15ynj - 3ynk) + (2xmi - 6xmj + 2xmk) = - i - 2j $
Make pair of terms with respect to the “i”, “j” and “k” terms –
 $ \Rightarrow \underline { - 6yni + 2xmi} + \underline {15ynj - 6xmj} \underline { - 3ynk + 2xmk} = - i - 2j $
Take common the respective terms –
 $ \Rightarrow i( - 6ny + 2mx) + j(15yn - 6x) + k( - 3yn + 2xm) = - i - 2j $
Now, compare the respective i,j and k terms on both the sides of the equation –
 $
   \Rightarrow - 6ny + 2mx = - 1\,{\text{ }}....{\text{ (A)}} \\
   \Rightarrow 15yn - 6mx = - 2{\text{ }}....{\text{ (B)}} \\
   \Rightarrow ( - 3yn + 2xm) = 0{\text{ }}....{\text{ (C)}} \\
  $
Simplify the equations to get the values of the terms “x” and “y”
Solve the equation (c)
 $
   \Rightarrow ( - 3yn + 2xm) = 0{\text{ }} \\
   \Rightarrow 3yn = 2xm\;{\text{ }}....{\text{ (D)}} \\
  $
Place the value of the equation (D) in the equation (A)
 $ \Rightarrow - 4mx + 2mx = 1\,{\text{ }} $
Simplify the equation –
 $
   \Rightarrow 2mx = 1\,{\text{ }} \\
   \Rightarrow {\text{x = }}\dfrac{1}{{2m}} \\
  $
Similarly place the above value in the equation (A)
 $ \Rightarrow - 6ny + 2mx = - 1 $
 $ \Rightarrow - 6ny + 2m\left( {\dfrac{1}{{2m}}} \right) = - 1 $
Like terms from the multiplicative and the division part cancel each other.
 $ \Rightarrow - 6ny + 1 = - 1 $
When the term is moved from one side to another, sign also changes from negative to positive and vice-versa.
 $
   \Rightarrow - 6ny = - 1 - 1 \\
   \Rightarrow - 6ny = - 2 \\
  $
Minus sign cancel each other from both the sides of the equation, and make the unknown “y” the subject.
 $
   \Rightarrow y = \dfrac{2}{{6n}} \\
   \Rightarrow y = \dfrac{1}{{3n}} \\
  $
Because, we assume $ 0 < x < 1 $ and $ 0 < y < 1 $
 $ \Rightarrow 0 < \dfrac{1}{{2m}} < 1{\text{ and }}0 < \dfrac{1}{{3n}} < 1 $
Simplification implies –
 $ \Rightarrow m > \dfrac{1}{2}{\text{ and n}} > \dfrac{1}{3}{\text{ }}....{\text{ (i)}} $
Now, the area of $ \left| {\Delta CHB} \right| = \dfrac{1}{2}\left| {(\overrightarrow {HB} \times \overrightarrow {CH} )} \right| $ .... (i)
Now, $ \overrightarrow {HB} = x\overrightarrow {AB} $
 $ \overrightarrow {HB} = xm(2i - 6j + 2k), $
Place the values $ \Rightarrow 2mx = 1\,{\text{ }} \Rightarrow {\text{mx = }}\dfrac{1}{2} $
 $
  \overrightarrow {HB} = \dfrac{1}{2}(2i - 6j + 2k) \\
  \overrightarrow {HB} = (i - 3j + k){\text{ }}....{\text{ (ii)}} \\
  $
Similarly, $ y\overrightarrow {CD} = yn( - 6i + 15j - 3k) $
Place the values - $ yn = \dfrac{1}{3} $
 $
  y\overrightarrow {CD} = \dfrac{1}{3}( - 6i + 15j - 3k) \\
  y\overrightarrow {CD} = ( - 2i + 5j - k){\text{ }}....{\text{ (iii)}} \\
  $
Find the cross-product by using equations (ii) and (iii)
 $ \overrightarrow {HB} \times \overrightarrow {CH} = \left| {\begin{array}{*{20}{c}}
  i&j&k \\
  1&{ - 3}&1 \\
  { - 2}&5&{ - 1}
\end{array}} \right| $
Expand the determinant-
 $ \overrightarrow {HB} \times \overrightarrow {CH} = i[( - 3)( - 1) - 5] - j[(1)( - 1) - ( - 2)(1) + k[(1)(5) - ( - 3)( - 2)] $
Simplify the above equation –
 $
  \overrightarrow {HB} \times \overrightarrow {CH} = i(3 - 5) - j( - 1 + 2) + k(5 - 6) \\
  \overrightarrow {HB} \times \overrightarrow {CH} = - 2i - j - k \\
  $
Find the magnitude –
 $
  \left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \left| { - 2i - j - k} \right| \\
   \Rightarrow \left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \sqrt {{{( - 2)}^2} + {{( - 1)}^2} + {{( - 1)}^2}} \\
  $
Square of negative terms gives the positive terms-
 $ \Rightarrow \left| {\overrightarrow {HB} \times \overrightarrow {CH} } \right| = \sqrt {4 + 1 + 1} = \sqrt 6 $
Now, place the above value in the equation (i)
 $
  \left| {\Delta CHB} \right| = \dfrac{1}{2}\left| {(\overrightarrow {HB} \times \overrightarrow {CH} )} \right| \\
   \Rightarrow \left| {\Delta CHB} \right| = \dfrac{1}{2}(\sqrt 6 ) \\
  $
Simplify the above equation –
 $ \Rightarrow \left| {\Delta CHB} \right| = \dfrac{{\sqrt 6 }}{2} $
Hence, from the given multiple choices- all the given options are the correct answer.
So, the correct answer is “Option D”.

Note: Always remember the properties of the cross-product and expansion of the determinant and simplify taking care of the positive and the negative sign. Also, remember the square and square-roots and its simplification for the efficient and accurate solution.