Question

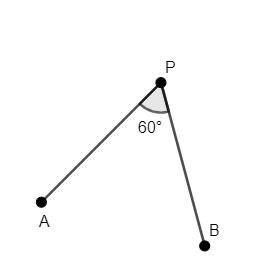
A, B are fixed points. State the locus of point \[P\] so that \[\angle APB={{60}^{\circ }}\].

Answer 1

Hint:Assume the coordinates of A and B and write the slope of line joining AP and BP. Use the tangent formula comparing angle between two lines to the slope of lines to get the locus of point P.

Complete step-by-step answer:
We have two fixed points \[A,B\]. We have to find the locus of point \[P\] such that \[\angle APB={{60}^{\circ }}\].
We will begin by assuming the points \[A=(a,b),B=\left( c,d \right)\]. We know that these two points are fixed.
Now, let’s assume that the coordinates of point \[P\] are \[\left( x,y \right)\].
We will now write the equation of slope of line joining \[AP\] and \[BP\].

We know that the slope of line joining any two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is \[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
Thus, by substituting \[{{x}_{1}}=a,{{y}_{1}}=b,{{x}_{2}}=x,{{y}_{2}}=y\] in the above equation, we get the slope of line joining \[AP\] as \[\dfrac{y-b}{x-a}\].
Let this slope be \[{{m}_{1}}=\dfrac{y-b}{x-a}.....\left( 1 \right)\].
Similarly, by substituting \[{{x}_{1}}=c,{{y}_{1}}=d,{{x}_{2}}=x,{{y}_{2}}=y\] in the above equation, we get the slope of line joining \[BP\] as \[\dfrac{y-d}{x-c}\].
Let this slope be\[{{m}_{2}}=\dfrac{y-d}{x-c}.....\left( 2 \right)\].
We know that the angle between two lines is \[{{60}^{\circ }}\].
We know that if the angle between two lines with slopes \[{{m}_{1}}\] and \[{{m}_{2}}\] is \[\theta \], then we have \[\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\].
Thus, we have \[\tan {{60}^{\circ }}=\left| \dfrac{\left( \dfrac{y-b}{x-a} \right)-\dfrac{y-d}{x-c}}{1+\left( \dfrac{y-b}{x-a} \right)\left( \dfrac{y-d}{x-c} \right)} \right|\].
Solving the above equation by substituting the value $\tan {{60}^{\circ }}=\sqrt{3}$ and removing modulus, we get \[\pm \sqrt{3}=\dfrac{\left( \dfrac{y-b}{x-a} \right)-\dfrac{y-d}{x-c}}{1+\left( \dfrac{y-b}{x-a} \right)\left( \dfrac{y-d}{x-c} \right)}\].
Thus, we have \[\pm \sqrt{3}\left( \left( x-a \right)\left( x-c \right)+\left( y-d \right)\left( y-b \right) \right)=\left( y-b \right)\left( x-c \right)-\left( y-d \right)\left( x-a \right)\].
On further solving, we get \[\pm \sqrt{3}{{x}^{2}}\mp \sqrt{3}x\left( a+c \right)\pm \sqrt{3}ac\pm \sqrt{3}{{y}^{2}}\mp \sqrt{3}y\left( b+d \right)\pm \sqrt{3}bd=xy-cy-bx+bc-xy+ay+dx-ad\].
Simplifying the above equation, we have \[\pm \sqrt{3}{{x}^{2}}\pm \sqrt{3}{{y}^{2}}+x\left( b-d\mp \sqrt{3}\left( a+c \right) \right)+y\left( c-a\mp \sqrt{3}\left( b+d \right) \right)+ac+bd-bc+ad=0\].
Thus, the locus of point \[P\] is of the form \[\alpha {{x}^{2}}+\alpha {{y}^{2}}+\beta x+\gamma y+\delta =0\].
Here, we observe that the values of \[\alpha ,\beta ,\gamma ,\delta \] are fixed depending on the co-ordinates of \[A=(a,b),B=\left( c,d \right)\].

Note: We can’t solve this question without writing the slopes of lines and using the formula relating angle between two lines to the slopes of lines. We will get different locus of P depending on the values of the coordinates of A and B.