Question

A 12 ohm resistor and a 0.21 henry inductor are connected in series to an AC source operating at 20 volts, 50 cycle/second. What is the phase angle between the current and the source voltage?

\[
  {\text{A}}{\text{. }}{30^0} \\
  {\text{B}}{\text{. }}{40^0} \\
  {\text{C}}{\text{. 8}}{0^0} \\
  {\text{D}}{\text{. 9}}{0^0} \\
 \]

Answer 1

Hint: Here we will proceed by finding the inductive reactance of the given inductor which will give the value of net impedance in the circuit. Then, we will use trigonometric rules in the impedance diagram.

Step By Step Answer :
Formulas Used- ${{\text{X}}_{\text{L}}} = \omega {\text{L}} = 2\pi {\text{fL}}$, $\pi = \dfrac{{22}}{7}$, ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$, $\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$, \[{\cos ^{ - 1}}\left( {\cos \phi } \right) = \phi \] and $\cos \left( {\dfrac{{\text{2}}}{{5\sqrt 5 }}} \right) = {80^0}$.

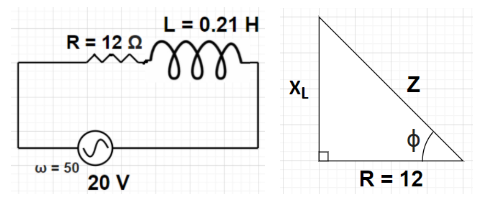
Given, Resistance R = 12 $\Omega $
Inductance L = 0.21 H
Frequency of AC voltage source f = 50 cycles/second

Let Z denote the overall impedance of the circuit and $\phi $ be the phase angle between the current and the source voltage.
As we know that the inductive reactance ${{\text{X}}_{\text{L}}}$ of the inductor having inductance L is given by

Inductive reactance ${{\text{X}}_{\text{L}}} = \omega {\text{L}} = 2\pi {\text{fL}}$
By substituting $\pi = \dfrac{{22}}{7}$, f = 50 cycles/second and L = 0.21 H in the above formula, we get

$ \Rightarrow {{\text{X}}_{\text{L}}} = 2\left( {\dfrac{{22}}{7}} \right)\left( {50} \right)\left( {0.21} \right) = 66{\text{ }}\Omega $

The impedance triangle for the given circuit is as shown in the figure.

According to Pythagoras theorem in any right angled triangle, we can write

${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$

Using the above formula in the drawn impedance triangle (which is also a right angled triangle), we have

$
  {{\text{Z}}^2} = {\left( {{{\text{X}}_{\text{L}}}} \right)^2} + {{\text{R}}^2} \\
   \Rightarrow {{\text{Z}}^2} = {\left( {{\text{66}}} \right)^2} + {\text{1}}{{\text{2}}^2} \\
   \Rightarrow {\text{Z}} = \sqrt {4356 + 144} \\
   \Rightarrow {\text{Z}} = \sqrt {4500} \\
   \Rightarrow {\text{Z}} = 30\sqrt 5 {\text{ }}\Omega \\
 $

In any right angled triangle, we can write

$\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$

Using the above formula in the drawn impedance triangle, we have

\[
  \cos \phi = \dfrac{{\text{R}}}{{\text{Z}}} \\
   \Rightarrow \cos \phi = \dfrac{{{\text{12}}}}{{{\text{30}}\sqrt 5 }} \\
   \Rightarrow \cos \phi = \dfrac{{\text{2}}}{{5\sqrt 5 }} \\
 \]

By taking inverse cosine trigonometric function on both sides, we get

\[ \Rightarrow {\cos ^{ - 1}}\left( {\cos \phi } \right) = {\cos ^{ - 1}}\left( {\dfrac{{\text{2}}}{{5\sqrt 5 }}} \right)\]
Using the formula \[{\cos ^{ - 1}}\left( {\cos \phi } \right) = \phi \] in the above equation, we get

\[ \Rightarrow \phi = {\cos ^{ - 1}}\left( {\dfrac{{\text{2}}}{{5\sqrt 5 }}} \right) = {80^0}\] [$\because \cos \left( {\dfrac{{\text{2}}}{{5\sqrt 5 }}} \right) = {80^0}$ ]

Therefore, the required phase angle between the current and the source voltage is \[{80^0}\].

Hence, option C is correct.

Note: In any resistance, the current and voltage will be in the same directly making an angle between them equal to 0 degree. In any inductor, the voltage leads the current (or the current lags the voltage) by 90 degrees. In any capacitor, the current leads the voltage (or the voltage lags the current) by 90 degrees.