Question

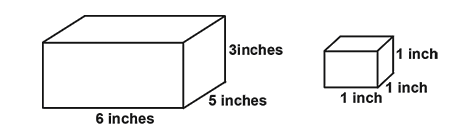
How many 1 inch cubes will completely fill the carton shown?

Answer 1

Hint: This is the formula for the volume of a cuboidal box
\[Volume{\text{ }} = {\text{ }}length \times width\; \times height\]
Volume of a cubical box can be found out by
\[Volume{\text{ }} = {\text{ }}length \times length\; \times length\]

Complete step by step solution: Start by putting a layer of blocks on the bottom of the box. Since the box is \[6\] inches long you can place \[6\] blocks along the front edge of the box. Then you can place a second row of \[5\] blocks behind it and again another row of \[5\] blocks behind the second row. You have placed \[6 \times \;5{\text{ }} = {\text{ }}30\] blocks on the bottom layer of the box.
The box is \[3\] inches high so you can put a second layer of \[30\] blocks on top of the first layer and then a third layer of \[30\] blocks to fill the box. Hence you have filled the box with \[3 \times \;30{\text{ }} = {\text{ }}90\], one cubic inch blocks.
Hence the volume of the box is \[36\] cubic inches and you obtained the number \[90\] from \[6 \times \;5 \times 3{\text{ }} = {\text{ }}90\] that is the length times the width times the height.
Also, we can use the formula \[Volume{\text{ }} = {\text{ }}length \times width\; \times height\]
to calculate the volume of the box, which is \[90\]

Note: Carton of length \[6\] inch- \[6\] number of \[1\] inch cube can come.
Width= \[5\] inch- \[5\] cube will fill. Height=\[3\] inch- \[3\] cube will fill.
So, total number of cubes is\[6 \times \;5 \times 3{\text{ }} = {\text{ }}90\]
The number of One-inch cubes that can be filled in a bigger one can be calculated just by dividing the volume of the bigger box with the smaller one.