Sonometer

Sonometers have been used as demonstration experiments for a very long time. The monochord was actually created by Pythagoras in the seventh century B.C. A French instrument maker named Albert Marloye improved the monochord in the middle of the nineteenth century, and the result was the differential sonometer. Both the monochord and the sonometer can be demonstrated. There are many different experiments that can be run.

The sonometer was used to show how the tension, length, and mass per unit length of the string affect the frequency of the sound produced when it is plucked. The transverse standing wave of the string is what produces the sound. One metre-long hollow box makes up the sonometer. A sonometer is a tool that displays the link between the tension, length, and mass per unit length of a string and the frequency of the sound produced when it is plucked. The principle involved in sonometer is resonance.

History

The Sumerian empire's texts contain the earliest mention of a sonometer or monochord. The sonometer is thought to have been devised by Pythagoras in the sixth century BCE. The "Celestial Monochord," a musical tuner, was created by Robert Fludd in 1618. Since then, the sonometer has been developed with the goal of producing a musical tuning instrument.

What does a Sonometer Actually Do?

Sonometer is the name for a tool used to measure sound waves. The device is used to show the connection between the tension, length, and mass per unit length of the string and the frequency of the sound it makes when it is pulled. The transverse standing wave of the string is what produces the sound. See below the sonometer diagram.

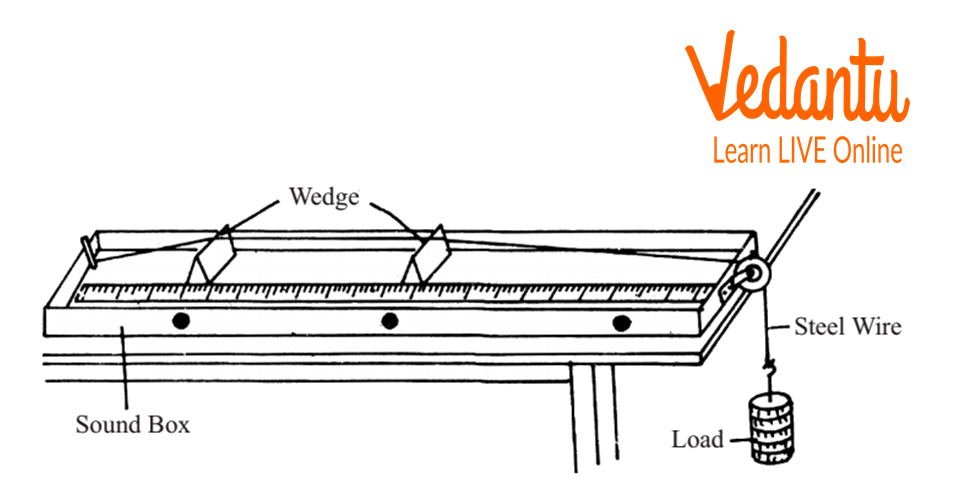
Sonometer

Any instrument that measures the vibration frequency, tension, density, or diameter of the wire, or that examines relationships between these characteristics, using a thin metallic wire stretched across two bridges that are often mounted on a soundboard. It goes by the term monochord as well.

A device for measuring rock stress uses a piano wire connected between two bolts in the rock; any change in pitch after destressing is noticed and used to determine stress.

The Sonometer's Constructing

• One metre-long hollow box makes up the sonometer.

• The inside of this hollow box is secured with a strong metallic rope.

• The first end of the string is attached to the hook with the aid of a pulley, and the second end is attached to the weight hanger.

• Because there is only one string used, the monochord is given a name.

• To increase the tension, weights are attached to the string's free end.

• To change the vibrating length of the stretched string, two adjustable knives are positioned and their locations are changed proportionately.

Using the Sonometer

The type of wave produced in a sonometer wire is standing transverse waves. In addition to nodes, anti-nodes are also created.

The sonometer's operation is mathematically described as follows:

Let l represent the vibrating element's length.

l = λ/2

λ = 2l

Let f be the frequency of the vibrating object. M stands for mass per unit length, and T stands for string tension. Then,

\[F = \dfrac{\nu }{\lambda }\]

The mass per unit length is calculated as where is the density of the material and \[d\] is the diameter of the string = density × area \[ = \pi {r^2}\rho = \pi \rho {{\rm{d}}^2}/4\]

\[\begin{array}{l}{\rm{F}} = \dfrac{v}{\lambda }\\ = \dfrac{1}{{2l}}\sqrt {\dfrac{{\dfrac{T}{{\rho \pi {{\rm{d}}^2}}}}}{4}} \;\\{\rm{F}} = \dfrac{l}{{ld}}\sqrt {\dfrac{T}{{\pi p}}} \end{array}\]

A Stretched String's Transverse Vibration Laws

The laws of transverse vibrations on a stretched string can be divided into two groups:

State First Law of Vibrating String – The Length Law

As long as the mass per unit length and the string tension is constant, the law of length states that the frequency of a stretched string's vibration and its resonating length fluctuates inversely.

As long as the mass per unit length and the string tension is constant, the law of length states that the frequency of a stretched string's vibration and its resonating length fluctuates inversely.

\[f \propto \dfrac{1}{{{\rm{ length }}}}\]

The Second Law of Vibrating String is the Tension Law - The Tension Law

The law of tension states that the frequency of vibration of a stretched string and the square root of its tension fluctuates directly as long as the resonating length and the mass per unit length of the string is constant.

\[f \propto 1\sqrt T {\rm{ (Tension) }}\]

The Mass Law

According to the law of mass, a stretched string's frequency of vibration and the square root of its mass per unit length varies inversely proportionally when the length and tension are both constant.

\[f \propto \dfrac{1}{{\sqrt {{\mathop{\rm mass}\nolimits} (m)} }}\]

How Precisely Does a Sonometer Work?

We already know that the sonometer is used to show the connection between frequency and the tension, length, and mass per unit length of the string. A sonometer can therefore be used to identify the following things:

• The frequency of the tuning fork.

• The frequency of the alternating current.

• The tension of the string.

• The unknown mass of the object hanging from the ceiling.

• What aspect does a standing wave have?

• Standing waves can be found, for example, in stringed instruments.

Solved Problems

Example 1: There is a tension T and a length l of a sonometer wire. If the second harmonic becomes equal to the fundamental frequency of the first example after reducing the tension to half of its original value and modifying the length, then the new length of the wire is

a) \[\dfrac{l}{{\sqrt 2 }}\]

b) \[\sqrt 2 l\]

c) \[\dfrac{l}{2}\]

d) 2l

Solution: To solve this problem, we will substitute the given values in the sonometer formula.

Use the sonometer formula \[{f_n} = \dfrac{n}{{2l}}\sqrt {\dfrac{T}{m}} \], where fn is the frequency of nth mode, n is the mode number, l is the length of the wire, and T is the tension in the wire. The wire's mass per unit length is m.

If the tension is reduced to half, and the length becomes l1, then from the above condition,

\[\dfrac{1}{{2l}}\sqrt {\dfrac{T}{m}} = \dfrac{2}{{2{l_1}}}\sqrt {\dfrac{T}{{2m}}} \]

Neglect n as it is a constant.

\[ \Rightarrow {l_1} = 1\sqrt 2 \]

Example 2: A sonometer wire of length 0.5 m is stretched by a weight of 5 kg. The fundamental frequency of vibration is 100 Hz. Calculate the linear density of the wire.

Solution: Given l = 0.5 m, T= 5 kg=5×9.8= 49 N, n=100 Hz

We know \[n = \dfrac{1}{{2l}}\sqrt {\dfrac{T}{m}} \]

Therefore, linear density \[m = \dfrac{T}{{4{l^2}{n^2}}}\]

m = \[ = \dfrac{{49}}{{4{{(0.5)}^2}{{(100)}^2}}}\]

m = ×10^-3 k kg/m

Summary

One metre-long hollow box makes up the sonometer. The inside of this hollow box is secured with a strong metallic rope. The tool was used to show how the tension, length, and mass per unit length of the string affect the frequency of the sound produced when it is plucked. The transverse standing wave sound is produced by the string.