




How Does Light Refract Through Water and Prisms?
Refraction of light is a central concept in physics, impacting everything from how we see objects underwater to the creation of rainbows in the sky. In simple terms, when a beam of light travels from one transparent medium to another—like from air into glass or water—its path bends. This bending phenomenon, called refraction of light, not only shapes everyday experiences but also underlies critical technologies and natural wonders. In this article, you’ll explore the definition, causes, formulas, effects, and real-life examples of refraction of light, along with essential notes for Class 10 physics and practical applications.
What is Refraction of Light? (Definition & Basics)
Refraction of light definition: In physics, refraction of light refers to the change in direction that a light wave undergoes when it passes from one medium into another with a different optical density. This shift occurs because light changes speed when moving across the boundary of two materials, such as from air into water or glass.
For example, if you place a pencil in a glass of water, the pencil appears bent or displaced at the surface. This common observation is due to the refraction of light in water. Such examples of refraction of light illustrate how waves alter their path depending on the properties of the media they cross.
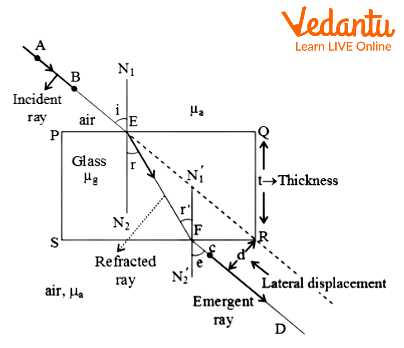
Learn how a glass slab demonstrates refraction of light
Why Does Refraction Occur? (Physical Cause & Effects)
The primary cause of refraction of light is the change in speed as light passes from one medium to another. Light travels faster in less optically dense media (like air) and slower in more optically dense materials (like water or glass). As the speed changes at the boundary, the wavefronts bend according to the optical properties of the media.
Some key effects and characteristics of refraction of light include:
- Objects appear shifted from their actual position (e.g., a submerged stone looks closer).
- Lenses focus or disperse light rays by refraction, forming images in cameras and eyes.
- Rainbows form when sunlight is refracted and dispersed by water droplets in the air.
- Apparent depth of pools and ponds differs from actual depth.
Refraction of light in physics is encountered in daily life and in complex devices like microscopes and telescopes. For visual learners, refraction of light images can help make this concept clearer.
Laws of Refraction & Key Formulas
Refraction of light obeys certain fundamental laws, often summarized as Snell’s Law (named after Willebrord Snellius):
Snell’s Law Formula (Refraction of Light Equation): $n_1 \sin\theta_1 = n_2 \sin\theta_2$
Where:
- $n_1$ = refractive index of the first medium
- $\theta_1$ = angle of incidence (in the first medium)
- $n_2$ = refractive index of the second medium
- $\theta_2$ = angle of refraction (in the second medium)
This equation helps predict how light will bend when it moves from one substance to another—critical for understanding refraction of light through a prism or a glass slab. For a comprehensive overview of optic-related formulas, see our curated list of Physics formulas for Class 12.
Step-by-Step: Derivation of Snell’s Law
- Let a light wave strike the boundary between two transparent media (e.g., air and water) at an angle of incidence $\theta_1$.
- Let the speed of light in medium 1 be $v_1$, and in medium 2 be $v_2$.
- The refractive index is given by $n = \frac{c}{v}$, where $c$ is the speed of light in vacuum.
- According to Huygens’ Principle, the ratio of sines of the angles equals the ratio of wave velocities: $\frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2}$.
- Since refractive index $n$ is inversely proportional to speed: $n_1 v_1 = n_2 v_2$.
- Combine results to get Snell’s Law: $n_1 \sin\theta_1 = n_2 \sin\theta_2$.
Examples and Illustrations of Refraction
Let’s look at some classic examples of refraction of light:
- A straw or pencil dipped in a glass of water appears broken at the water’s surface (refraction of light in water).
- Formation of rainbows is due to light refracting and dispersing inside raindrops (refraction of light rainbow example).
- Prisms splitting white light into its constituent colors work due to refraction of light through a prism (dispersion by prisms).
- Lenses in spectacles use refraction to correct vision, such as for hypermetropia or myopia.
If you are fascinated by colors, you might enjoy our guide on the VIBGYOR spectrum.
10 Notable Effects & 5 Applications of Refraction of Light
Ten effects of refraction of light:
- A coin at the bottom of a tank appears raised
- Mirage formation in deserts
- Starlight twinkling is partially due to atmospheric refraction
- Apparent bending of trees or poles when viewed at an angle from under water
- Formation of halos around the sun or moon
- Advance sunrise and delayed sunset
- Lenses focusing or diverging light in cameras and glasses
- Magnifying glasses and microscopes making small objects visible
- The sparkle of diamonds, due to high refraction
- Creation of optical fibers for high-speed communication
Five practical applications of refraction of light:
- Corrective eyewear: Glasses and contact lenses
- Magnifying devices: Simple and compound microscopes (microscope details)
- Telescopes for astronomy
- Cameras and photography equipment
- Optical fibers for high-speed data transmission
To understand more about how light waves function in various scenarios, explore our resource on wavelength of light.
Quick Notes for Refraction of Light | Class 10
Refraction of light Class 10 notes: When a ray of light passes obliquely from one transparent medium to another, it changes direction at the boundary. This bending is towards the normal when entering a denser medium (like air to glass) and away from the normal when entering a rarer medium (like water to air). The amount of bending depends on the refractive indices of both media and the angle of incidence.
Summary Table: Key Quantities in Refraction
| Quantity | Symbol | Typical Value |
|---|---|---|
| Refractive Index (Air) | $n_{air}$ | ~1.00 |
| Refractive Index (Water) | $n_{water}$ | ~1.33 |
| Refractive Index (Glass) | $n_{glass}$ | ~1.52 |
| Angle of Incidence | $\theta_1$ | Varies |
| Angle of Refraction | $\theta_2$ | Varies |
This table helps compare how refractive indices affect the way light bends in practical examples.
Numerical Example: Calculating the Angle of Refraction
Suppose a ray of light enters water from air. The angle of incidence in air ($\theta_1$) is $30^\circ$. Let $n_{air} = 1.00$ and $n_{water} = 1.33$. What is the angle of refraction ($\theta_2$)?
- Use Snell’s law: $n_{air} \sin \theta_1 = n_{water} \sin \theta_2$
- Substitute values: $1.00 \times \sin 30^\circ = 1.33 \times \sin \theta_2$
- $\sin 30^\circ = 0.5$
- $0.5 = 1.33 \times \sin \theta_2$
- $\sin \theta_2 = \frac{0.5}{1.33} \approx 0.376$
- $\theta_2 = \arcsin(0.376) \approx 22^\circ$
So, the refracted ray bends to about $22^\circ$ inside water.
Special Topics: Refraction in Rainbows, Prisms, and Destiny 2
Refraction of light becomes especially interesting in contexts like rainbows and prisms. When sunlight enters a raindrop, it refracts, reflects inside the droplet, and exits at an angle, dispersing light into its various colors—a beautiful demonstration of refraction of light rainbow effect. Similarly, refraction of light through a prism reveals the spectrum of white light (VIBGYOR).
Surprisingly, "refraction of light Destiny 2" refers to a gaming concept where light bending is used metaphorically within the Destiny 2 universe, indicating the broad cultural reach this physics topic enjoys.
Curious about related wave behaviors? Check out our guide to the concept of a wavefront and how waves propagate.
Conclusion: Why Refraction of Light Matters in Physics
In summary, refraction of light is a fundamental and fascinating topic in physics, explaining why objects look displaced under water, how lenses correct vision, and how spectacular rainbows form. Understanding refraction of light in physics helps unlock everything from simple classroom experiments to advances in optical technologies. Whether you’re a student reviewing refraction of light Class 10 notes, solving numerical problems, or simply observing the world, the principles and effects of refraction impact your life every day. Continue exploring the wonders of optics and light for deeper insight!
FAQs on Understanding the Refraction of Light in Physics
1. What is refraction of light?
Refraction of light is the bending or change in direction of a light ray as it passes from one medium to another due to a change in its speed.
- This occurs when light moves between materials of different optical densities, such as air to water or glass.
- The degree of bending depends on the refractive indices of the two media.
- Key terms include normal, angle of incidence, angle of refraction, and refractive index.
2. What causes the refraction of light?
Refraction is caused by the change in speed of light as it passes from one medium to another.
- Light slows down or speeds up depending on the optical density of the medium.
- When entering a denser medium, light bends towards the normal.
- When entering a rarer medium, light bends away from the normal.
3. State Snell’s Law of refraction.
Snell’s Law describes the relationship between the angles of incidence and refraction when light passes through two media.
- Snell’s Law states: n₁ sin i = n₂ sin r
- Where n₁ and n₂ are refractive indices, i is angle of incidence, r is angle of refraction.
- This law explains how the degree of bending depends on the properties of both media.
4. Give two examples of refraction of light in daily life.
Refraction of light occurs in many everyday situations.
- Pencil in water appears bent or broken at the water surface.
- Lenses in eyeglasses use refraction to correct vision.
- Other examples: coin appearing raised in water, mirage in deserts.
5. What is the refractive index?
The refractive index is a number that describes how much light slows down in a given medium compared to its speed in vacuum.
- It is calculated as n = c/v, where c is the speed of light in vacuum and v is the speed in the medium.
- Higher refractive index means light slows down more.
- Common values: air ~1.00, water ~1.33, glass ~1.5.
6. Why does a coin kept in water appear raised?
A coin in water appears raised due to refraction of light at the water-air interface.
- Light rays bend away from the normal when they move from water to air.
- This shift causes the coin to appear higher than its actual position.
7. How does the speed of light change when it moves from air to glass?
When light travels from air into glass, its speed decreases.
- Glass has a higher refractive index than air.
- Light slows down and bends towards the normal.
8. What is total internal reflection and when does it occur?
Total internal reflection occurs when a light ray in a denser medium hits the boundary at an angle greater than the critical angle and reflects entirely back into the medium instead of refracting.
- Occurs only when moving from denser to rarer medium (e.g., water to air).
- This is used in optical fibers and diamonds for brilliance.
9. What is the difference between reflection and refraction of light?
Reflection and refraction are two different ways in which light interacts with surfaces or media.
- Reflection is the bouncing back of light from a surface (like a mirror).
- Refraction is the bending of light as it passes from one medium to another due to a change in speed.
- Key differences: direction change, medium interface, optical density involved.
10. Explain with a diagram how a ray of light bends when passing from air to glass.
When a ray of light enters glass from air, it slows down and bends towards the normal due to a higher refractive index of glass.
- The angle of incidence is greater than the angle of refraction.
- A labelled diagram should show the incident ray, refracted ray, normal, and the angles involved.
- This process is called refraction and is subject to Snell’s Law.
11. Why do stars appear to twinkle at night?
Stars twinkle at night due to the refraction of light caused by the Earth's turbulent atmosphere.
- The varying densities in air continuously bend the star’s light path.
- This causes the apparent brightness and position of stars to change rapidly.
12. What are the practical applications of refraction of light?
Many everyday devices and technologies work on the principle of refraction of light.
- Lenses in eyeglasses and cameras
- Prisms and optical fibers
- Magnifying glasses and microscopes
- Mirages and other atmospheric phenomena





































