Introduction to Parallel Axis Theorem
Physics frequently deals with situations where objects rotate about an axis that passes through their centre of mass. It is usually simple to seek up the moment of inertia for the majority of objects of various forms when considering rotational motion about an object's centre of mass.
The moment of inertia is the lowest when the rotational axis is across the centre of mass. As the rotational axis's separation from the centre of mass widens, the moment of inertia grows.
The theorem makes it easy to connect any two parallel axes' moments of inertia by going through the centre of mass.
History of the Scientist/Theorem
The polymath Christiaan Huygens(14 April 1629 – 8 July 1695) first introduced the idea of the moment of inertia while researching a compound pendulum. Jakob Steiner(18 March 1796 – 1 April 1863) afterwards added his significant addition to this theorem. In honour of Christiaan Huygens and Jakob Steiner, the parallel axis theorem is frequently referred to as the Huygens-Steiner theorem.
Christiaan Huygens(14 April 1629 – 8 July 1695)
Parallel Axis Theorem Definition
According to the "Parallel Axis Theorem," a body's moment of inertia about any axis is equal to the product of that body's mass and the square root of the distance between the axes, as well as its moment of inertia about a parallel axis that passes through its centre of mass.
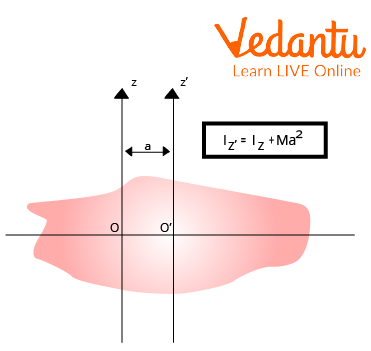
Parallel Axis Theorem
What is the Formula of the Theorem of Parallel Axis?
Mathematically the parallel axis theorem can be expressed as,
\[I = {I_0} + M{s^2}\]\[\]
Where,
I denote the body's moment of inertia concerning any axis.
Io denotes the body’s moment of inertia concerning the parallel axis through its centre of mass.
M denotes the mass of the body.
S denotes the distance between the two parallel axes.
Parallel Axis Theorem Proof
Consider two parallel axes, one of which, designated \[OY\], passes through the rigid body's centre of mass, and the other, designated \[{O_1}{Y_1}\], which is situated \[s\] distance away from \[OY\]. Let's take into account a small mass \[dm\] that is located \[R\]from the axis \[OY\] and \[{R_1}\]from the axis \[{O_1}{Y_1}\].
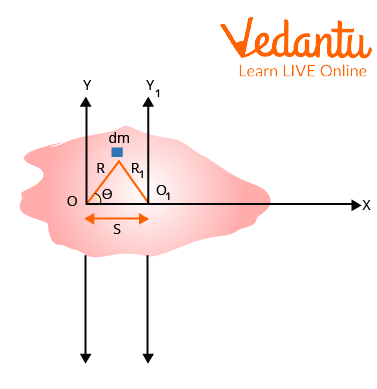
Parallel Axis Theorem Proof
The rigid body's total mass is \[M = \int {dm} \]. Therefore, the rigid body's moment of inertia about the axes \[OY\] and \[{O_1}{Y_1}\] is,
\[\begin{array}{l}I{}_0 = \int {{R^2}} dm{\rm{ and}}\\I = \int {{R_1}^2} dm\end{array}\]
The above figure allows us to write,
\[R_1^2 = {R^2} + {s^2} = 2sR\cos \theta \]
Therefore,
\[\begin{array}{l}I = {\int {{R_1}} ^2}dm\\I = \int {{R^2}} dm + \int {{s^2}} dm + \int {2sR} \cos \theta dm\end{array}\]
\[\begin{array}{l}I = {I_0} + M{s^2} + \int {2sR} \cos \theta dm\\{\rm{[}}{I_0} = \int {{R^2}} dm{\rm{ and }}\int {{s^2}} dm = M{s^2}{\rm{] }}\end{array}\]
In this case, \[R\cos \theta \] is the mass element's x-coordinate about the mass centre.\[\int {R\cos \theta } dm\], then, is the body's moment of mass concerning the axis of its centre of mass, \[OY\]. Since the body's centre of mass serves as the foundation for equilibrium,
\[\int {R\cos \theta } dm = 0\]
Therefore, the final equation will be as follows,
\[I = {I_0} + M{s^2}\]\[\]
Hence Proved.
Limitations of Parallel Axis Theorem
The usefulness of the parallel axis theorem is constrained.
The object's mass should be evenly distributed along the reference axis.
Application of Parallel AxisTheorem
The moment of inertia of a rigid body is determined using the parallel axis theorem in conjunction with any axis.
Any object in rotation can have its moment of inertia determined using the parallel axis theorem.
Solved Examples
1. If a body has a moment of inertia of 30 kgm2 along an axis perpendicular to its centre of gravity and a mass of 50kg. What is that body's moment of inertia along a different axis that is parallel to and 50cm distant from the current axis?
Ans: Given data:
\[\begin{array}{l}{I_0} = 30kg{m^2}\\M = 50kg\\s = 20cm = 0.2m\end{array}\]
We have the formula,
\[I = {I_0} + M{s^2}\]\[\]
Replace every known value in the formula above.
\[\begin{array}{l}I = 30 + 50 \times {(0.2)^2}\\ \Rightarrow I = 30 + 2\\ \Rightarrow I = 32kg{m^2}\end{array}\]
2. How much inertia does a stick with a mass of 100 g, and a length of 10 cm have?
Ans. Given data:
\[\begin{array}{l}M = 50g = 0.05kg\\s = 20cm = 0.2m\end{array}\]
The general formula for the moment of inertia of a rod with mass (M) and length (L) and an axis that passes through the rod's centre is;
\[I = (\frac{1}{{12}})M{s^2}\]
Therefore,
\[\begin{array}{l}I = \frac{1}{{12}} \times 0.05 \times 0.2\\I = 0.000833Kg{m^2}\end{array}\]
3. Find the moment of inertia of a solid sphere with a mass of 30kg and a radius of 2m around an axis that is 5m distant from the surface using the parallel axis theorem.
Ans. Given data:
\[\begin{array}{l}M = 30Kg\\R = 2m\\s = 5m\end{array}\]
The moment of inertia of a solid sphere with mass m and radius R about an axis that goes through its centre is \[{I_0} = \frac{2}{5}m{R^2}\].
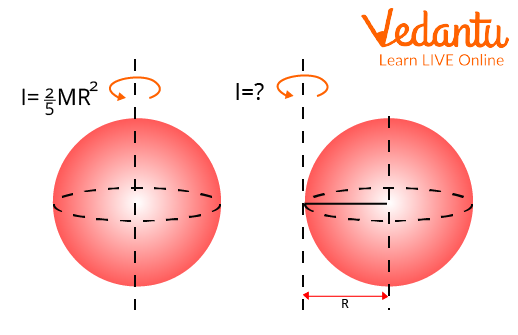
Solid Sphere
Therefore by the parallel axis theorem,
\[I = {I_0} + M{s^2}\]\[\]
Replace every known value in the formula above.
\[\begin{array}{l}I = \frac{2}{5}(30){(2)^2} + 30 \times {(5)^2}\\ \Rightarrow I = 48 + 750\\ \Rightarrow I = 798kg{m^2}\end{array}\]
Important Points to Remember
To apply the parallel axis theorem, the following considerations must be made.
Considered axis A and B must be parallel.
The axis B must go through the body's centre of mass, and
The distance between them must be the shortest possible.
Important Formulas to Remember From Theorem
The general formula for the Parallel axis theorem with mass (M) and distance(s),
\[I = {I_0} + M{s^2}\]\[\]
The general formula for the moment of inertia of a rod with mass (M) and length (L) and an axis that passes through the rod's centre is;
\[I = (\frac{1}{{12}})M{s^2}\]
Conclusion
The parallel axis theorem implies the sum of the moment of inertia through the mass centre and the product of the mass and square of the angle perpendicular to the rotational axis. The moments of inertia about various axes are connected by this theorem. But the usefulness of this theory is limited, though. For instance, the reference axis in the parallel axis theorem should pass through the object's centre of mass.
FAQs on Parallel Axis Theorem
1. Define the gyrating radius or radius of gyration when the centre of mass is located where the axis of rotation passes.
The distance from the axis of rotation to the location where the body's total mass is thought to be concentrated, allowing the moment of inertia about the axis to remain constant, is known as the radius of gyration. The dispersion of an object's parts is known as gyration, which is represented by the symbol K. And the value of the radius of gyration or gyrating radius when the centre of mass is located where the axis of rotation posses is minimal, but it is not exactly zero.
2. What is the moment of inertia, and what is the parallel axis theorem's formula for it?
Each particle's mass multiplied by the square of its separation from the axis of rotation yields the body's moment of inertia. It follows that the moment of inertia is a physical characteristic that combines the mass and dispersion of the particles around the rotational axis. Observe that different moment of inertia result from rotation about various axes of the same body. And we can calculate the moment of inertia using the parallel axis theorem. Here is the equation for that:
\[I = {I_0} + M{s^2}\]\[\]
3. Differentiate between parallel axis theorem and perpendicular axis theorem.
Both theorems deal with the moment of inertia, but how they are applied differs. According to the perpendicular axis theorem, the sum of any two perpendicular axes of the body that meet the first axis determines the moment of inertia for any axis that is perpendicular to the plane. While the parallel axis theorem is used to determine the moment of inertia of a rigid body whose axis is parallel to the axis of the known moment and which is located via the body's centre of gravity.