An Introduction to Bernoulli’s Theorem
Bernoulli’s theorem is the principle of energy conservation for perfect fluids in steady, or streamline, flow and is the basis for many engineering applications. This was first derived in 1738 by a Swiss mathematician, Daniel Bernoulli.
Bernoulli’s Equation
Bernoulli's equation is used to solve any problems involving incompressible fluid flow. The Bernoulli equation applies to the various measuring devices like Venturi meter, Nozzle meter, Orifice meter, Pitot tube, and its applications to flow measurement from takes, within pipes, and in open channels.
History of the Daniel Bernoulli
Daniel Bernoulli \[1700–1782\] was a Dutch scientist who studied in Italy before settling in Switzerland. Born from a family of mathematicians, his father, Johann Bernoulli, was one of the early pioneers of calculus, and his uncle, Jacob Bernoulli, was the first to discover probability theory. Bernoulli derived his well-known Bernoulli Theorem in 1738.
Daniel Bernoulli (1700–1782)
Statement of the Bernoulli’s Theorem
Bernoulli’s theorem, also known as Bernoulli’s principle, states that the whole mechanical energy of the moving fluid, which includes gravitational potential energy of elevation, fluid pressure energy, and kinetic energy of fluid motion, remains constant.
$p+\dfrac{1}{2}\rho {{v}^{2}}+\rho gh$= constant
This equation is known as Bernoulli’s equation.
Bernoulli’s Theorem Derivation
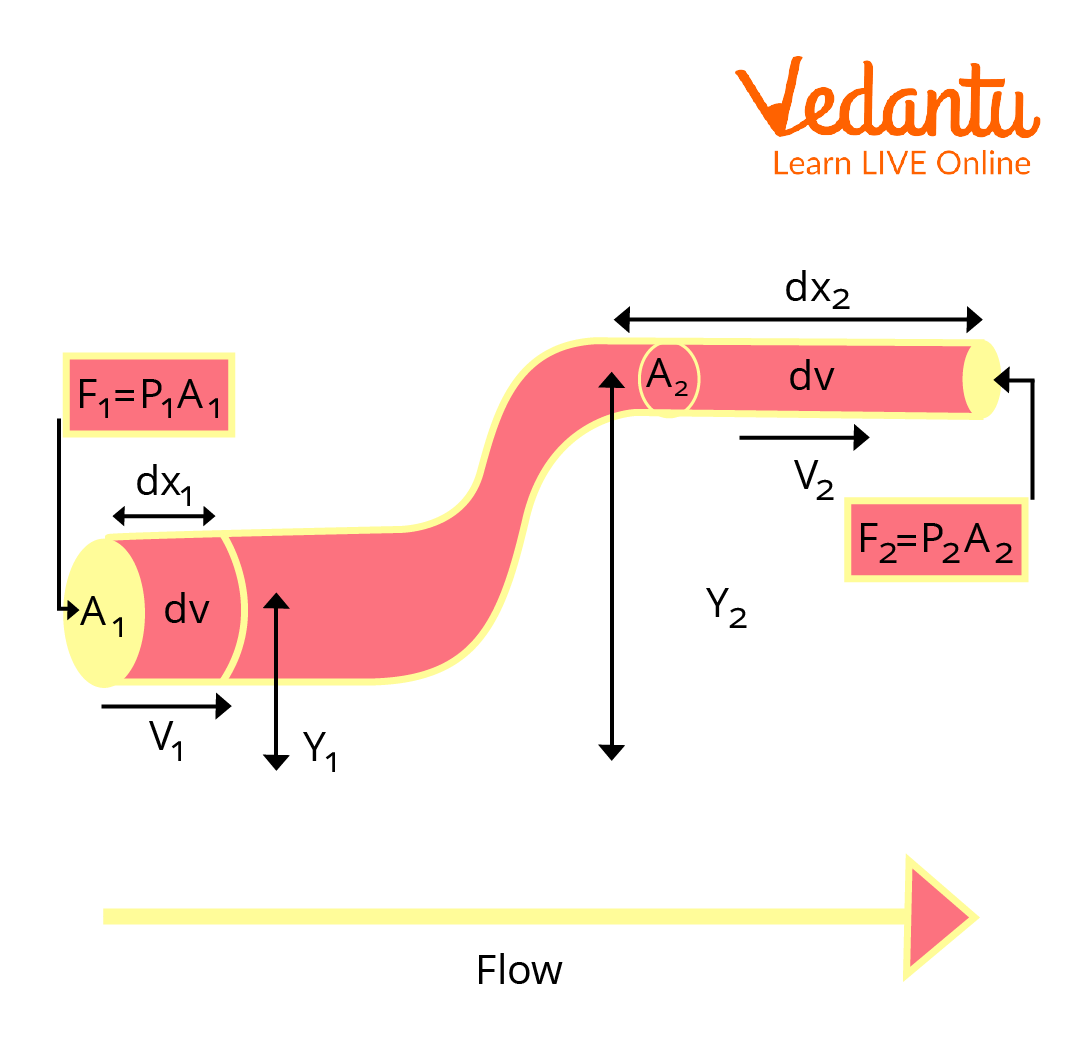
Bernoulli’s Principle
According to Bernoulli’s theorem, the fluid's work can be expressed as:
dW = F1dx1 - F2dx2
\[dW = {p_1}{A_1}d{x_1} - {p_2}{A_2}d{x_2}\]
\[dW = {p_1}dv - {p_2}dv =\left( {p_1} - {p_2}\right)dv\]
The energy of the system is equal to the sum of the change in fluid’s kinetic energy and the change in fluid’s potential energy.
\[dW = dK + dU\] ……(1)
As known, the work done on the fluid was owing to the conservation of change in gravitational potential energy and change in kinetic energy. The fluid's kinetic energy change is represented as:
\[dK = \dfrac{1}{2}{m_2}^2{v_2}^2-\dfrac{1}{2}{m_1}^2{v_1}^2\]
\[dK = \dfrac{1}{2}\rho {dv}\left({v_2}^2 - {v_1}^2\right)\]
Change in the potential energy can be expressed as:
\[dU={m_2}g{y_2}-{m_1}g{y_1}=\rho g {dv} \left({y_2}-{y_1}\right)\]
Substitute all the obtained and known values in equation (1):
\[dW=dK+dU\]
\[\left({p_1}-{p_2}\right)dv=\dfrac{1}{2}\rho {dv}\left({v_2}^2 - {v_1}^2\right)+{m_2}g{y_2}-\rho g {dv} \left({y_2}-{y_1}\right)\]
\[\left({p_1}-{p_2}\right)=\dfrac{1}{2}\rho \left({v_2}^2 - {v_1}^2\right)+{m_2}g{y_2}-\rho g \left({y_2}-{y_1}\right)\]
On rearranging the above equation, we get
\[{p_1}+\dfrac{1}{2} \left(\rho {v_1}^2\right)+\rho g {y_1}={p_2}+\dfrac{1}{2} \left(\rho {v_2}^2\right)+\rho g {y_2}\]
This is the required Bernoulli’s equation and p is the static pressure of the fluid across the cross-section, $\rho$ is the density of the fluid, g is the acceleration due to gravity, v is the mean velocity of the fluid flow, and h is the elevation head of the cross-section.
Limitations of Bernoulli’s Theorem
Due to friction, the fluid particle velocity is greatest in the middle of a tube and decreases gradually towards the tube's direction. As a consequence, because particles of the liquid velocity are not consistent, the liquid's mean velocity must be employed.
This formula can be used to enhance a liquid supply's efficiency. But in turbulent or non-steady flows, it is ineffectual.
This theorem is typically used for low viscosity fluids.
Application of Bernoulli's Theorem
Bernoulli's principle can successfully explain a wide range of applications in current science and life. Among them are:
One of the best Bernoulli's theorem applications is that it is used to solve any problems involving incompressible fluid flow.
It is also used to estimate factors like pressure and fluid speed.
In an aeroplane, Bernoulli's principle can be used. This hypothesis, for example, explains why aeroplane wings are curled upward and ships must run away from each other as they pass.
Solved Examples
1. Which of the following fluid flows does not obey Bernoulli's law?
Unsteady
Turbulent
Rotational
All of the above
Ans: The correct answer is Option D because the equation only applies to streamlining and steady flows.
2. Water flows smoothly in a closed pipe system, with one point having a speed of \[3.0m{s^{ - 1}}\] and another higher having a speed of \[4.0m{s^{ - 1}}\]. What is the pressure at the upper point if the lower pressure is stated as \[20kPa\]?
Ans:
Given,
\[{p_1} = 20kPa = 20\times {10^3}~N/{m^2}\]
\[\rho = {10^3}kg{m^{ - 3}}\]
\[{v_1} = 3m{s^{ - 1}}\]
\[{y_1} = 0m\]
\[{v_2} = 4m{s^{ - 1}}\]
\[{y_2} = 1m\]
Applying Bernoulli’s equation,
\[{p_1}+\dfrac{1}{2} \left(\rho {v_1}^2\right)+\rho g {y_1}={p_2}+\dfrac{1}{2} \left(\rho {v_2}^2\right)+\rho g {y_2}\]
\[\Rightarrow \left(20\times {10^3}\right)+\left(\dfrac{1}{2} \times {10^3}\times{3^2}\right)+0={p_2}+\left(\dfrac{1}{2} \times{10^3}\times {4^2}\right)+\left({10^3}\times {10} \times {1}\right)\]
\[\Rightarrow {24500}={p_2}+{18000}\]
\[\Rightarrow {p_2}={24500}-{18000}=6500\]
\[\therefore {p_2}=6.5kPa\]
3. Water flows through a pipe with widths of \[20cm\] and \[10cm\] in sections \[1\]and \[2\], respectively. The flow rate through the pipe is \[2\] litres per second. Section \[1\] is \[6\] metres above the datum, and \[2\] is \[4\] metres above the datum. If the pressure in the section is \[39.24\] N/cm2, calculate the pressure intensity in the section.
Ans: Given,
For section \[1\],
\[{D_1} = 20cm = 0.2m\]
\[{A_1} = \dfrac{\pi }{4}\]
\[{D_1}^2\] = \[\dfrac{\pi }{4} \] 0.2m2 = 0.0314m2
\[{P_1} = 39.24\dfrac{N}{{c{m^2}}} = 39.24 \times {10^4}\dfrac{N}{{{m^2}}}\]
\[{Z_1} = 6m\]
For section \[2\],
\[{D_2} = 10cm = 0.1m\]
\[{A_2} = \dfrac{\pi }{4} {D_1}^2\] = \[\dfrac{\pi }{4} \] 0.1m2 = 0.0078m2
\[{P_2} = ?\]
\[{Z_2} = 4m\]
Discharge or rate of flow, \[Q = 35l/{\mathop{\rm s}\nolimits} = 35 \times {10^{ - 3}}{m^3}/s\].
\[Q = {A_1}{V_1} = {A_2}{V_2}\]
For \[Q = {A_1}{V_1}\]
\[{V_1} = \dfrac{Q}{{{A_1}}} = \dfrac{{35 \times {{10}^{ - 3}}}}{{0.0314}}\]
\[{V_1} = 1.114~m/s\]
And for \[Q = {A_2}{V_2}\]
\[{V_2} = \dfrac{Q}{{{A_2}}} = \dfrac{{35 \times {{10}^{ - 3}}}}{{0.00785}}\]
\[{V_2} = 4.456~m/s\]
Applying Bernoulli’s equation in sections \[1\] and \[2\],
\[\dfrac{{{p_1}}}{{\rho g}} + \dfrac{{{v_1}^2}}{{2g}} + {z_1} = \dfrac{{{p_2}}}{{\rho g}} + \dfrac{{{v_2}^2}}{{2g}} + {z_2}\]
\[\dfrac{{39.24 \times {{10}^4}}}{{1000 \times 9.81}} + \dfrac{{{{1.114}^2}}}{{2 \times 9.81}} + 6 = \dfrac{{{p_2}}}{{1000 \times 9.81}} + \dfrac{{{{4.456}^2}}}{{2 \times 9.81}} + 4\]
\[40 + 0.063 + 6 = \dfrac{{{p_2}}}{{9810}} + 1.012 + 4\]
\[46.063 = \dfrac{{{p_2}}}{{9810}} + 5.012\]
\[\dfrac{{{p_2}}}{{9810}} = 46.063 - 5.012\]
\[\dfrac{{{p_2}}}{{9810}} = 41.051\]
\[{p_2} = 40.27~N/{{cm}^2}\]
Important Points to Remember
It is vital to note that when obtaining this equation, we assume that there is no loss of energy due to friction if we adopt the energy conservation principle. However, there is an energy loss due to internal friction induced by fluid flow. This will result in some energy loss.
Important Formulas to Remember from Bernoulli’s Theorem
\[{p_1} + \dfrac{1}{2}p{v_1}^2pg{y_1} = {p_2} + \dfrac{1}{2}p{v_2}^2pg{y_2}\]
p is the static pressure of the fluid across the cross-section.
\[\rho \] is the density of the fluid.
g is the acceleration due to gravity.
v is the mean velocity of the fluid flow.
y is the elevation head of the cross-section.
Conclusion
Bernoulli's principle gives insight into a variety of applications, making it a vital building block not just in the field of Physics but also in other branches of study. Bernoulli's theorem and its applications are broad and varied. The best approach to grasp these various applications is to have an open debate about the idea itself.
FAQs on Bernoulli’s Theorem and Its Equation
1. Explain how, according to the Bernoulli Principle, slower flowing fluids generate more pressure (force) than faster moving fluids.
Bernoulli's principle, often known as Bernoulli's equation, will apply to ideal fluids. As a result, pressure and density are inversely proportional. This means that a slow-moving fluid will exert more pressure than a faster moving fluid. The discovery of this concept was made by Swiss scientist Daniel Bernoulli while testing with fluid inside pipes. His experiment discovered that as the fluid's speed increases, its internal pressure falls. Therefore, according to this principle, slower flowing fluids generate more pressure force than faster moving fluids.
2. What are the assumptions for Bernoulli’s equation?
The assumptions of Bernoulli’s equation are as follows:
The fluid is excellent or perfect, with zero viscosity.
The flow is constant (the velocity of every liquid particle is uniform).
While flowing, there is no energy loss.
It is not possible to compress the flow.
Irrotational flow is present.
Except for gravity, there is no external force acting on the liquid.
3. Why is Bernoulli's theorem ineffective in turbulent or non-steady flows?
Bernoulli's principle applies to liquids in their ideal condition, where pressure and density are inversely proportional. However, turbulent flow is a sort of fluid gas or liquid flow in which the fluid fluctuates or mixes irregularly with time. In these instances, the speed of the fluid at a place is constantly changing in magnitude and direction, which is why Bernoulli's equation does not apply to non-steady or turbulent liquid flow. And the equation is only applicable in areas of constant, incompressible flow when frictional forces can be ignored.
