Work Time Formula

We must first correctly comprehend "Time and Work." Think about having a deadline for your work. So how long will you wait for that? How are you going to compute that? Your effectiveness will determine these kinds of things. Therefore, it is a calculation of how much work may be accomplished in a given amount of time.

Have you thought about how long it will take to finish the project if we hire someone to help us? Efficiency is the word that is most commonly used today. As you are aware, everyone craves speed these days. What if you want to make any team or worker more productive? The formulas for work, time, and efficiency will be used to compute it.

Work

What is work? What do you think about work? Look, every little thing we do to achieve something can be called work. For example, you are learning this, for what you are doing! So that you can get good marks in class, Or make your future bright. It is also a “Work”. People usually refer to work as physical work.

Unit of work is measured in ‘Joule’ or ‘J’.

A Man working

Time

If you are doing some work, time is equally important. As you have to complete your work in a certain time. If you are in school you have to complete your syllabus within 1 year. That is how time is also an important thing to be cared for. Unit of time is measured in ‘Second’ or ‘s’. Now let’s see time and work together.

Shows Time

Work Time Relation

Everyone works for a limited period of time. And thereafter they get results of their work. And the result is usually based on how much work you have done in a certain amount of time. For example – If you are filling a bottle with water in 1 minute and you do that work for 15 minutes. You will have 15 bottles filled. That’s how work happens with respect to time.

Time spent and work done are directly proportional. Additionally, efficiency, one-day work, and work rate eliminate the proportionality sign.

Work is directly proportional to time,

\[{\rm{W\alpha T}}\]

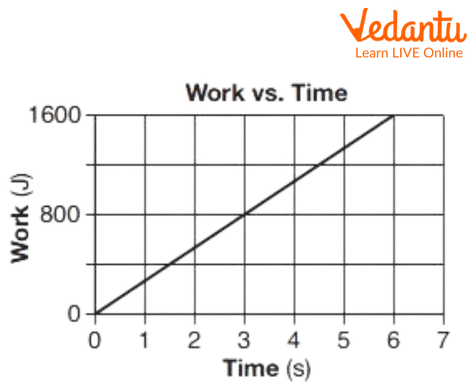
Work and Time Graph

Efficiency

Efficiency is the “total work done” in “Total time” Or can say how much work you can complete in a given time. You will get many questions mentioned as the efficiency of A is twice the efficiency of B or A takes half the time taken by B to do the same work. This all conveys the same meaning. It is inversely proportional to Time,

\[{\rm{E}}\alpha \frac{1}{{\rm{T}}}\].

Work and Time Relation

Formula:

Total work done \[ = \] Time \[ \times \] Efficiency

The above formula can be understood in simple words that the total work done is equal to the times multiplied by efficiency.

We will understand this by solving the upcoming examples:

Man Work Problems

Steps to solve man work problems:

Q. If \[{{\rm{M}}_{\rm{1}}}\] number of people work \[{{\rm{W}}_{\rm{1}}}\], in \[{{\rm{D}}_{\rm{1}}}\] days, working \[{{\rm{T}}_{\rm{1}}}\] hours each day. And a number of \[{{\rm{M}}_{\rm{2}}}\] people working on a work \[{{\rm{W}}_{\rm{2}}}\] completes in \[{{\rm{D}}_{\rm{2}}}\] days, working \[{{\rm{T}}_{\rm{2}}}\] hours each day. Then we can find any of the single missing values by equating these two equations.

W \[ = \] days \[ \times \] hours each day \[ \times \] number of men

W \[ = \] D \[ \times \] T \[ \times \] M

1 \[ = \] \[\frac{{[{\rm{D}} \times {\rm{T}} \times {\rm{M}}]}}{{\rm{W}}}\]

And we will get the same equation for both cases,

So,

\[\frac{{[{{\rm{D}}_1} \times {{\rm{T}}_1} \times {{\rm{M}}_1}]}}{{{{\rm{W}}_{\rm{1}}}}} = \frac{{[{{\rm{D}}_2} \times {{\rm{T}}_{_2}} \times {{\rm{M}}_2}]}}{{{{\rm{W}}_2}}}\]

Because this equation is basically = 1.

The problem basically deals with the man's efficiency, or how much work a man can do in a certain period of time.

Solved Examples

1: Work can be completed by 12 men in 24 days and 12 women in 12 days. In how many days would the 12 men and 12 women working together complete the work?

Solution: As 12 men complete the job in 24 days, the work amount

\[12 \times 24 = 288\]

288 man-days.

For this group of men, the total work amount is 288 man-days. If 6 such men work, the number of days they would take to finish the work would simply be

\[\frac{{288}}{6}\]= 48

48 days.

Coming back to our problem, similarly for women, the amount of work is 144 woman days. It leads to,

144 womandays \[ = \] 288 mandays,

Or, 1 womanday \[ = \] 2 mandays.

Or, 12 woman days \[ = \] 24 man-days.

Thus if 12 men and 12 women work together for a day, it is equivalent to

\[[12 + 24] = 36\]

\[[12 + 24] = 36\] men working on the job for 1 day.

The total work amount being 288 man-days, the number of days taken to complete the job, in this case, will be,

\[\frac{{288}}{{36}} = 8\]

8 days.

2: A can do a piece of work in 24 days and B in 20 days but with the help of C they finish the work in 8 days. C alone can do the work in how many days?

Solution: Using work formula here \[\frac{1}{{\rm{A}}} + \frac{1}{{\rm{B}}} + \frac{{\rm{1}}}{{\rm{C}}} = \frac{1}{8}\]

\[\frac{1}{C} = \frac{1}{8} - \left[ {\frac{1}{A} + \frac{1}{B}} \right]\]\[ \Rightarrow \]\[\frac{1}{C} = \frac{1}{8} - \frac{1}{{24}} - \frac{1}{{20}}\];

\[ \Rightarrow \frac{1}{C} = \frac{1}{{30}}\]

So,

\[{\rm{C}} = 30\]

C can do this work in 30 days.

3: “A” can do a piece of work in 20 days. He did that for 5 days and then “B” finished it in 15 days. In how many days can A and B together finish the work?

• 24 days

• 18 days

• 10 days

• 15 days

Solution – A’s 5 days work \[ = \frac{5}{{20}} = \frac{1}{4}\].

Remaining work \[ = 1 - \frac{1}{4} = \frac{3}{4}\]

This work was done by “A” in 15 days. A does \[\frac{3}{4}\]th of the work in 15 days, He will finish the work in \[15 \times \frac{4}{3} = 20\]days A & B together would take \[\left[ {\frac{{\rm{1}}}{{\rm{A}}} + \frac{1}{B}} \right]\frac{1}{{20}} + \frac{1}{{20}} = \frac{2}{{20}} = \frac{1}{{10}}\].

So A&B together will take 10 days to complete the work.

4: It takes ‘H’ hours to mow a lawn. In one hour what part of the lawn is mowed?

• \[{\rm{H}} - 1\]

• \[1 - {\rm{H}}\]

• \[\frac{H}{{[1 + H]}}\]

• \[\frac{{\rm{1}}}{{\rm{H}}}\]

Solution – Total time to mow a lawn is H hour.

Then in one hour it will mow \[ = \frac{1}{{\rm{H}}}\] .

Conclusion

Work and time formulas are very important and practical in daily life. as we can assess the efficiency of every employee or piece of equipment or the proper amount of time for planning. and has an approximate estimate of how long the current task will take. This article has covered all the essential formulas and examples that can be used to determine someone's time and effort. These are all facts that are currently within our grasp. So let's move on to the problems.