




How to Identify the Base and Exponent in a Number
It is very easy to 2 and 2. But if someone asks you to add 2 5 or 6 times or more than that? Wouldn't it be a little difficult for you? We can still add 5 or 6 times, but if we have to add the number 125 times, wouldn’t be a very lengthy and tedious task? Don’t worry, we are not here to give you a worksheet on adding a number 125 times, but we are here to discuss the shortcut of doing that. Go ahead and learn the basic concepts behind the Base and Exponents. Exponents are simply a shorthand method of indicating that you want to multiply any number by itself a number of times. Base number indicates which number is being multiplied. In other words, we can say that Exponent of a number indicates how many times a base number should be multiplied.
For example, we know how to calculate the expression 2 x 2 x 2 x 2. Here, 2 is multiplied by itself four times. This can be simply written as 24. Both values are equal to 16.
2 x 2 = 4
2 x 4 = 8
2 x 8 = 16
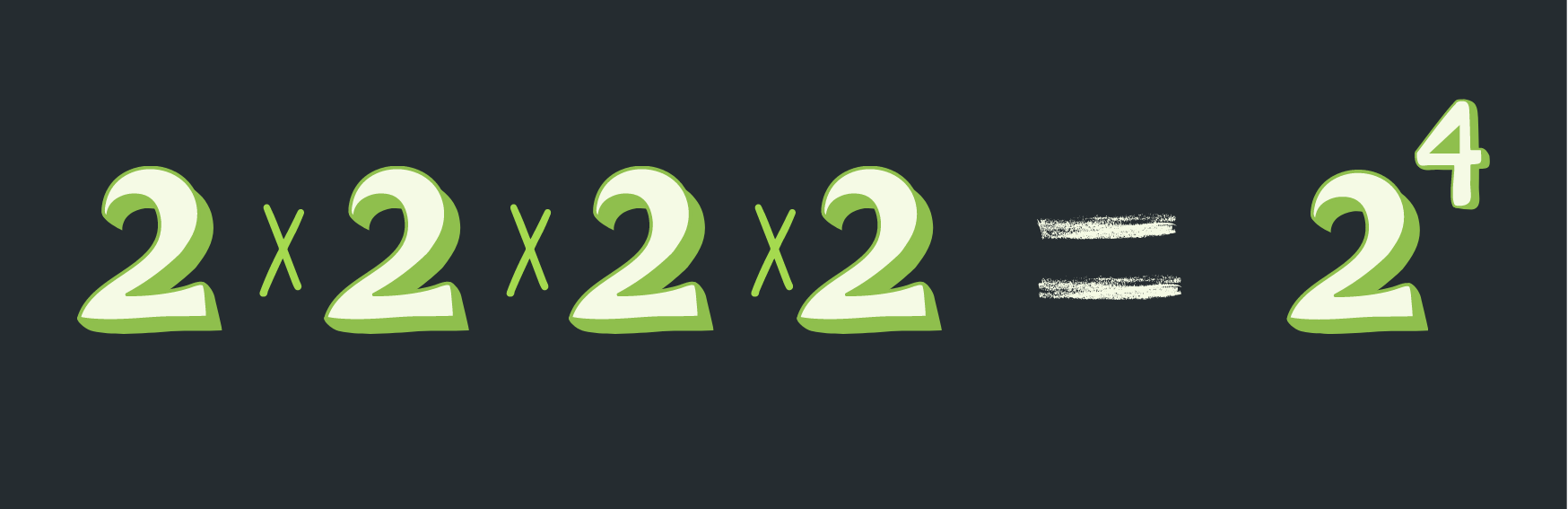
Image Showing 2 Multiplied by 2 for Four Times is Equal to 2 Raised to the Power of 4
Exponent is written in the top right corner of the base number as a little number. In the above example, 24, read as “2 to the power 4” or “2 raised to the power of 4”. In this given example, 2 is the base and 4 is the exponent.
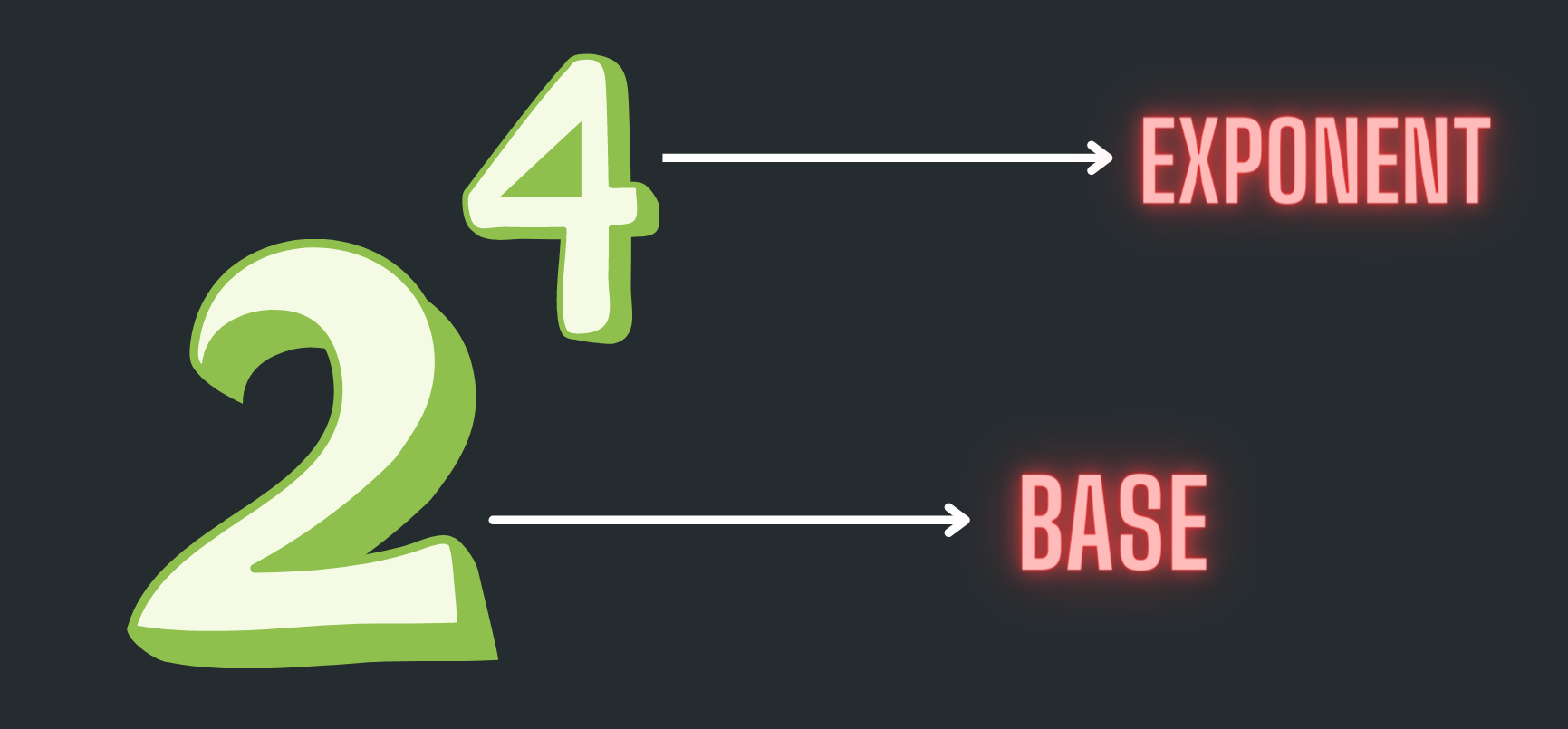
Image Shows the Base 2 with an Exponent 4
Power
The term "power" refers to the repeated multiplication of the same component. Base and Exponent together are called “Power”. The expanded form of a power will give the factors. This is shown in the below image with the example of “5 raised to the power of 3”.
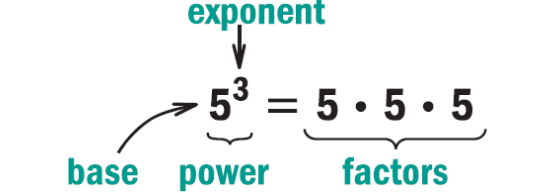
Image Shows a Base and an Exponent Makes a Power Which is Split into Factors
Use of Exponents
Using Exponents, we can represent large or small numbers in a simplified manner.
Examples of representing numbers in simplified form using exponents:
8: 8 can be written as 2 x 2 x 2 = 4 x 2 = 8. The simplified form of 8 is 23
81: 81 can be written as 3 x 3 x 3 x 3. So, the simplified form of 81 is 34
2: 2 is a prime number which is in its simplified form. This can be represented as 21
Writing multiplications in Exponents
1. 3 x 3 x 3
Here, 3 is multiplied by itself for 3 times. This can be written as 33 in exponent form.
2. 8 x 8
Here, 8 is multiplied by itself for 2 times. This can be written as 82 in exponent form.
3. 6 x 6 x 6 x 6 x 6
Here, 6 is multiplied by itself for 5 times. This can be written as 65 in exponent form.
How to write a given Exponent with a base?
1. “8 to the power of 5”
In “8 to the power of 5”, we write 8 in the base and the exponent 5 will be written in the top right corner of 8 like below.
85
2. “1 to the power of 9”
In “1 to the power of 9”, we write 1 in the base and the exponent 9 will be written in the top right corner of 1 as shown below.
19
3. “9 to the power of 5”
In “9 to the power of 5”, we write 9 in the base and the exponent 5 will be written in the top right corner of 5 like below.
95
Identifying Base and Exponent and Reading the Exponents?
1. 45
Here, Base is 4 and the Exponent is 5. So, this is generally read as “4 to the power of 5.”
2. 106
Here, Base is 10 and the Exponent is 6. This is read as “10 to the power of 6”.
3. 13100
Here, Base is 13 and the Exponent is 100. This is read as “13 to the power of 100”.
4. (-8)2. This is an exponent with a negative base.
Here, Base is (-8) and the Exponent is 2. This is read as “-8 to the power of 2”.
Note: Parentheses make a difference. Be careful while observing the negative base. Note that -82 is not same as -82. In -82, “-8” is not the base, 8 the base but in (-8)2 base is “-8”.
Special Cases of Reading the Exponents
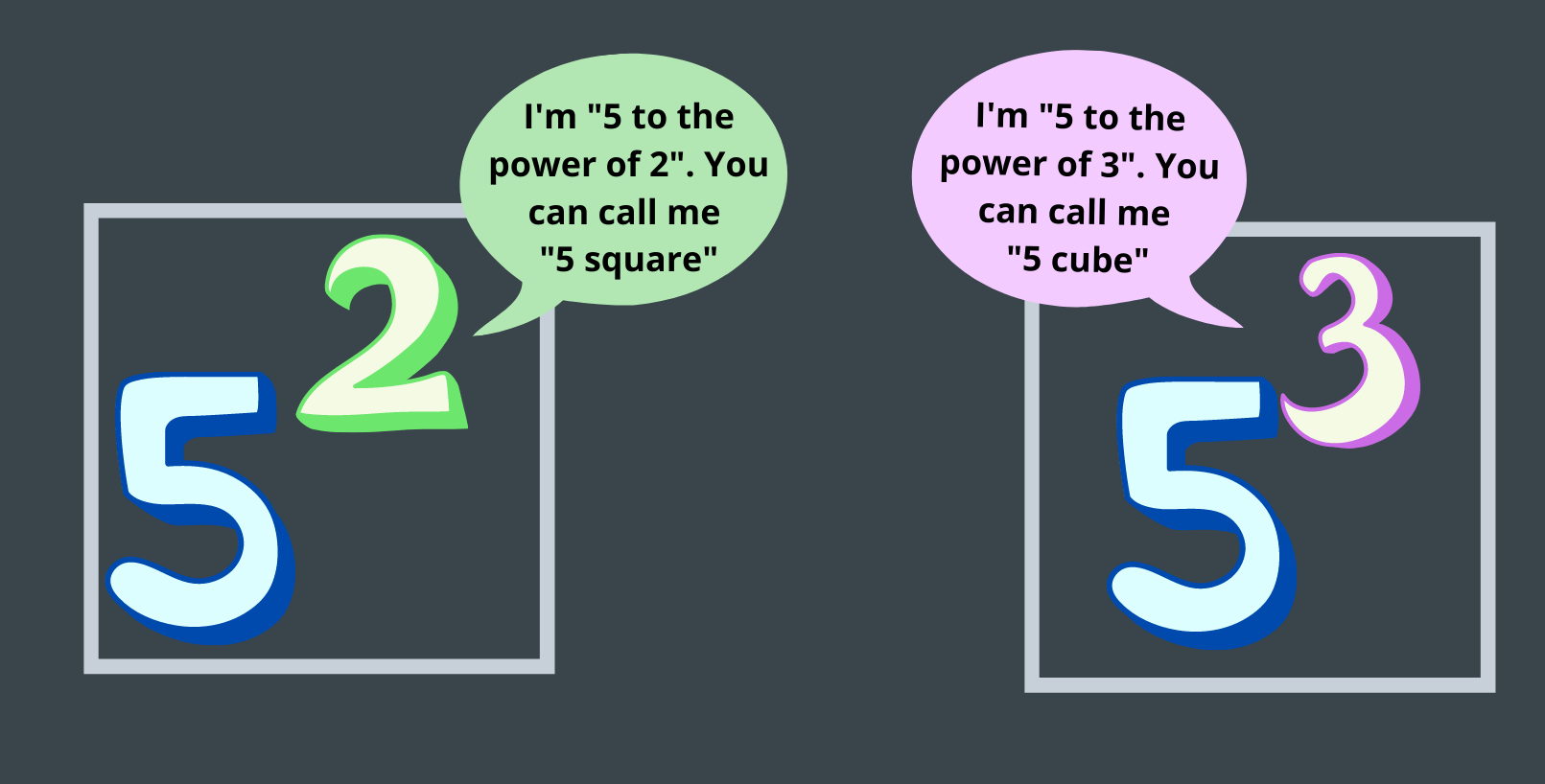
Image Shows Special Cases of Reading Exponents
1. If a base of an exponent is equal to 2, then that can also be read as base square.
Eg: 102; Here the base is 10 and the exponent is 2. We can read this as “10 square” or “10 to the power of 2”.
2. If a base of an exponent is equal to 3, then that can also be read as base cube.
Eg: 103; Here the base is 10 and the exponent is 3. We can call it as “10 cube” or “10 to the power of 3”
3. Power of 10 (or) base 10 with any exponent:
It's a lot of fun to multiply the powers of tens. When multiplying a whole number by a power of ten, simply count how many zeros you have and add them to the full number. Exponents will tell you how many zeros you'll need.
Try These Yourself
Read and write the given powers in the below table and Fill in the blanks.
Answers to Cross Verify:
1) The value of 24 is equal to 2 x 2 x 2 x 2 = 16
2) 32 in words is “Three to the power of Two” or “Three square”.
3) The value of 44 is equal to 4 x 4 x 4 x 4 = 256
4) 53 in words “Five to the power of Three” or “Five cube”
5) The value of 101 is equal to 10.
FAQs on What Is the Base of an Exponent?
1. What is an exponent?
An exponent can be defined as a method through which we can express large numbers in terms of power. For example, 6 multiplied six times i.e., 6 x 6 x 6 x 6 x 6 can be written as 65, which is equal to 30.
2. What is the Base of an Exponent?
The base number specifies the number that is being multiplied. The exponent, which is a small number written just above to the right of the base number, shows how many times the base number has been multiplied. In “5 to the power of 7”, written as 57 the base is 5 and the exponent is 7.

















