Tangent To Hyperbola Formula Derivation And Solved Examples
A hyperbola is a set of all points (x, y) such that the difference of the distances between (x, y) and two different points is constant. A hyperbola has two vertices that lie on the axis of symmetry known as the transverse axis. The transverse axis of the hyperbola can either be horizontal or vertical. In this article, we will get to know about the different types of equations of the tangent to hyperbola like the equation of tangent of hyperbola in slope form, equation of tangent of hyperbola in parametric form, the chord of contact of hyperbola, and point of contact of the tangent to a hyperbola.
Equation of Hyperbola
The general equation of hyperbola can be represented as $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$.
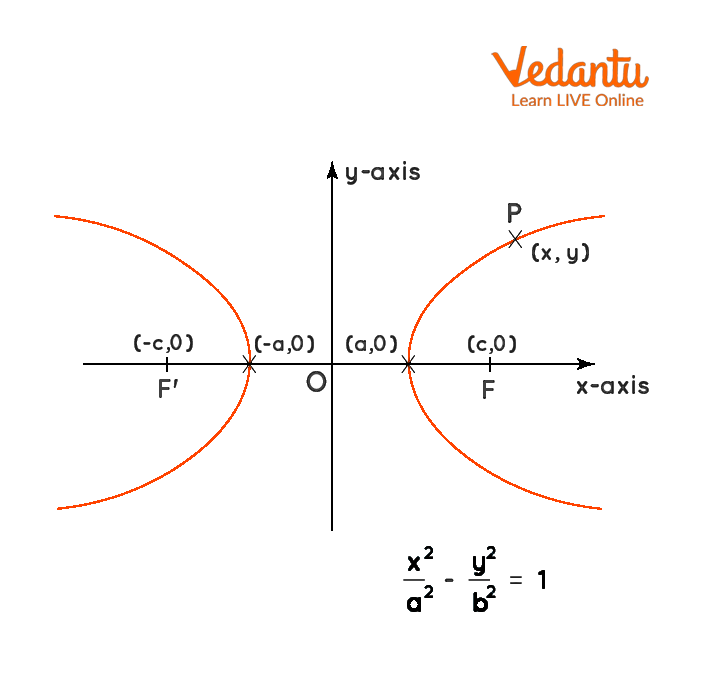
Hyperbola
Point Form Equation of a Tangent to Hyperbola
In this form, the tangent is drawn from the point of contact of the tangent to the hyperbola. Let’s say the point of contact of the hyperbola to tangent is $(x_{1},y_{1})$, then the equation of the tangent to hyperbola will be $\dfrac{xx_{1}}{a^{2}}+\dfrac{yy_{1}}{b^{2}}=1$.
Equation of Tangent to Hyperbola in Slope Form
This type of equation gives us the equation of the tangent of hyperbola in terms of the slope of the line “m”. The equation is $y=mx\pm \sqrt{a^{2}m^{2}-b^{2}}$
This equation is also called “The condition of tangency”.
Equation of Pair of Tangents in Hyperbola
When the equation of the hyperbola is $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$, then the pair of tangents can be represented using $SS_{1}=T^{2}$ i.e
$(\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}-1)(\dfrac{x_{1}^{2}}{a^{2}}-\dfrac{y_{1}^{2}}{b^{2}}-1)=(\dfrac{xx_{1}}{a^{2}}+\dfrac{yy_{1}}{b^{2}}-1)$
Chord of Contact of Hyperbola
A chord of contact is a chord passing through endpoints of tangents drawn from a point
$(x_{1},y_{1})$ to the hyperbola. The equation of chord of contact of hyperbola will be $\dfrac{xx_{1}}{a^{2}}+\dfrac{yy_{1}}{b^{2}}=1$ .
Equation of Tangent to Hyperbola in Parametric Form
The parametric coordinates of any hyperbola can be represented as$a sec\theta, btan\theta$ and the equation of a tangent to hyperbola will be $\dfrac{x(asec\Theta )}{a^{2}}-\dfrac{y(atan\Theta )}{b^{2}}=1$
Interesting Facts
When an object, let's say a jet, moves faster than the speed of sound, it creates a conical form of a wave in space and that wave intersects the ground, the curve we get from that intersection is a hyperbola.
The cooling towers are generally made of hyperbolic shape to achieve 2 things: first, the least amount of material used to make it and second, the structure should be strong enough to withstand strong winds.
Solved Examples
Example 1. Find the equation of a tangent to the hyperbola $x^{2}-4y^{2}=4$ which is parallel to the line $x+2y=0$.
Solution: Equation of hyperbola : $\dfrac{x^{2}}{4}-\dfrac{y^{2}}{1}=1$ ,
So ,$a^{2}=4\Rightarrow a=2$
$b^{2}=1\Rightarrow a=1$
The slope of the given line will be $\dfrac{1}{2}$. Now, using the condition of tangency we will calculate the value of c.
$c^{2}=a^{2}m^{2}-b^{2}$
$c^{2}=2^{2}(-\dfrac{1}{2}^{2})-(1)^{2}$
$c=0$
So, the equation of tangent will be
$y=-\dfrac{1}{2}x$
$x+2y=0$
Example 2. Find the equation of the chord of contact of the hyperbola $\dfrac{x^{2}}{6}-\dfrac{y^{2}}{2}=1$ if the tangents are drawn from (3,2).
Solution: We know that The equation of chord of contact of a hyperbola is $\dfrac{xx_{1}}{a^{2}}-\dfrac{yy_{1}}{b^{2}}=1$. So,
$\dfrac{x(3)}{6}-\dfrac{y(2)}{2}=1$
$\dfrac{x}{2}-\dfrac{y}{1}=1$
$x-2y=2$is the required equation of chord of contact.
Practice Questions
Question 1. What is the value of m for which $y=mx+6$ is tangent to the hyperbola $\dfrac{x^{2}}{100}-\dfrac{y^{2}}{49}=1$?
Ans: $\sqrt{\dfrac{17}{20}}$,$- \sqrt{\dfrac{17}{20}}$
Question 2. A common tangent to $9x^{2}-16y^{2}=144$ and $x^{2}+y^{2}=9$ is____.
Ans: $y=3\sqrt{\dfrac{2}{7}}x\pm \dfrac{15}{\sqrt{7}}$
Summary
The article summarises the concept of the chord of contact and tangents as a hyperbola. We learnt about different types of forms of tangents and how to find the equation of these tangents, then we did some examples to brush up on our concepts and get a better understanding of the topic. We hope to have helped you clear your doubts on this topic and learn something new. Do try out the solved examples and practise questions to evaluate your understanding of the concepts discussed here.
FAQs on Various Forms Of Tangents In Hyperbola Explained Clearly
1. What is the equation of the tangent to a hyperbola at a given point?
The equation of the tangent to a hyperbola at a point (x₁, y₁) on the curve is obtained using the standard tangent form of that hyperbola. For example, for the hyperbola x²/a² − y²/b² = 1, the tangent at (x₁, y₁) is:
xx₁/a² − yy₁/b² = 1.
This formula is valid only when (x₁, y₁) satisfies the hyperbola equation. It is one of the most commonly used forms of tangents in hyperbola problems.
2. What is the slope form of the tangent to a hyperbola?
The slope form of the tangent to the hyperbola x²/a² − y²/b² = 1 is y = mx ± √(a²m² − b²).
This form is used when the slope (m) of the tangent is known.
- It represents all tangents having slope m.
- The condition for real tangents is a²m² − b² ≥ 0.
- This form is helpful in solving problems involving slope of tangent and family of tangents.
3. How do you find the equation of a tangent to a hyperbola using differentiation?
To find the tangent using calculus, first compute the derivative dy/dx and then use the point-slope form of a line.
For x²/a² − y²/b² = 1:
- Differentiate implicitly: (2x/a²) − (2y/b²)(dy/dx) = 0
- So, dy/dx = (b²x)/(a²y)
- At point (x₁, y₁), slope m = (b²x₁)/(a²y₁)
- Use point-slope form: y − y₁ = m(x − x₁)
4. What is the parametric form of the tangent to a hyperbola?
The parametric form of the tangent to x²/a² − y²/b² = 1 is x secθ / a − y tanθ / b = 1.
Here, the point on the hyperbola is:
- x = a secθ
- y = b tanθ
5. What is the condition for a line to be tangent to a hyperbola?
A line is tangent to the hyperbola if it intersects the curve at exactly one point.
For the line y = mx + c to be tangent to x²/a² − y²/b² = 1, the condition is:
c² = a²m² − b².
This condition ensures that the quadratic formed after substitution has equal roots, meaning the line touches the hyperbola at exactly one point.
6. What is the equation of tangent in intercept form for a hyperbola?
The intercept form of a tangent to x²/a² − y²/b² = 1 is x/a secθ − y/b tanθ = 1.
This form is derived from the parametric representation and is helpful when:
- Using trigonometric parameters
- Solving problems involving intercepts on coordinate axes
- Studying different forms of tangents in hyperbola
7. How do you find the tangent to a rectangular hyperbola?
For a rectangular hyperbola xy = c², the tangent at point (x₁, y₁) is xy₁ + yx₁ = 2c².
Steps:
- Ensure (x₁, y₁) satisfies xy = c².
- Use the standard tangent formula for rectangular hyperbola.
- This form is symmetric and simpler than the general hyperbola case.
8. What is the difference between tangent and normal to a hyperbola?
The tangent touches the hyperbola at one point, while the normal is perpendicular to the tangent at that point.
For x²/a² − y²/b² = 1 at (x₁, y₁):
- Slope of tangent = (b²x₁)/(a²y₁)
- Slope of normal = negative reciprocal
9. How do you find the pair of tangents from an external point to a hyperbola?
To find tangents from an external point (x₁, y₁), use the combined equation of tangents method.
For x²/a² − y²/b² = 1, replace x²/a² − y²/b² − 1 by T and use:
TT₁ = T²₁ (where T₁ is obtained by substituting (x₁, y₁)).
This gives a second-degree equation representing the pair of tangents from the external point.
10. What are the different forms of tangents in a hyperbola?
The different forms of tangents in a hyperbola include point form, slope form, parametric form, intercept form, and derivative form.
Common forms for x²/a² − y²/b² = 1:
- Point form: xx₁/a² − yy₁/b² = 1
- Slope form: y = mx ± √(a²m² − b²)
- Parametric form: x secθ / a − y tanθ / b = 1
- Rectangular hyperbola form: xy₁ + yx₁ = 2c²
