




How to Apply the Transitive Property: Step-by-Step Guide
The “Transitive Property” consists of two words: transitive and property. The meaning of the word transitive is to transfer one thing to another. The meaning of property is any characteristic that applies to a given set. We need three numbers or objects to apply transitive property. If object 1 is equal to object 2 and object 2 is equal to object 3, then according to the transitive property, object 1 is equal to object 3.
What is Transitive Property?
Transitive property states that if a, b, and c are all real numbers and a is equal to b and b is equal to c, then it implies that a is equal to c. The mathematical representation of transitive property is if a = b and b = c, then a = c.
General Formula of Transitive Property
The general formula of transitive property states that a, b, and c are an element of a set or collection of the same kind of objects. If a = b and b = c, then a = c.
To apply transitive property, we need at least three objects of the same kind. Suppose a and b are lengths of lines and c is the area of a triangle, then we cannot apply transitive property on a, b, and c.
Transitive Property of Equality
The transitive property of equality states that two real numbers are equal to each other and if one of them is equal to another real number, then the first real number is equal to the third real number. In another word, if x = y and y = z, then x = z.
For example, Jina and Tina have the same number of balloons which is 4. Oja has the same number of balloons as Tina. Thus, the number of balloons for Jina = the number of balloons for Tina and the number of balloons for Tina = the number of balloons for Oja. According to the transitive property: the number of balloons of Jina = the number of balloons of Oja = 4.
Transitive Property of Inequality
Transitive property is also applicable to inequalities.
Types of inequality: There are 4 types of inequalities. They are greater than, less than, greater than or equal to, and less than or equal to. Transitive property on all inequalities:
1) Greater Than:
If x is greater than y and y is greater than z, then x is greater than z.
For example, 5 is greater than 4, and 4 is greater than 3. According to the transitive property, 5 is greater than 3 which is correct.
2) Less Than:
If x is less than y and y is less than z, then x is less than z.
For example, -1 is less than 2, and 2 is less than 4. According to the transitive property, -1 is less than 4 which is correct.
3) Greater Than or Equal To:
If x is greater than or equal to y and y is greater than or equal to z, then x is greater than or equal to z. For example, 4 is greater than or equal to 3, and 3 is greater than or equal to 2. According to the transitive property, 4 is greater than or equal to 2.
4) Less Than or Equal To:
If x is less than or equal to y and y is less than or equal to z, then x is less than or equal to z. For example, 1 is less than or equal to 3, and 3 is less than or equal to 5. According to the transitive property, 1 is less than or equal to 5
Transitive Property of Congruence
The transitive property of congruence is applicable to the geometrical shape or 2-dimensional shape. It states that if a pair of angles or lines or triangles are congruent and one of them is congruent to a third angle or line or triangle, then all lines or angles, or triangles are congruent.
Transitive Property Examples
Example 1: Mina and Tina are twin sisters. Mina is 4 years old. Sana’s birth date is the same as Tina's. Since Mina and Tina are twin sisters, thus Age of Mina = the age of Tina. Again Sana’s birth date is the same as Tina's. So, the age of Tina = the age of Sana. According to the transitive property, Age of Mina = age of Sana = 4 years.
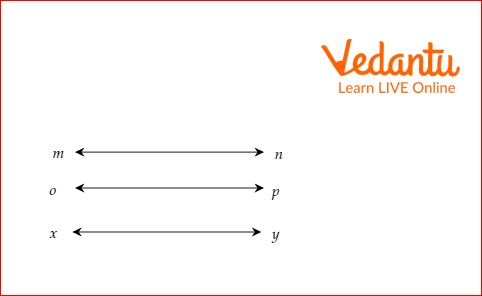
Example 2: The length of line segment mn is the same as the line segment op. Again, the length of line segment op is the same as the line segment xy. In other words, mn = op and op = xy. According to the transitive property, mn = xy.
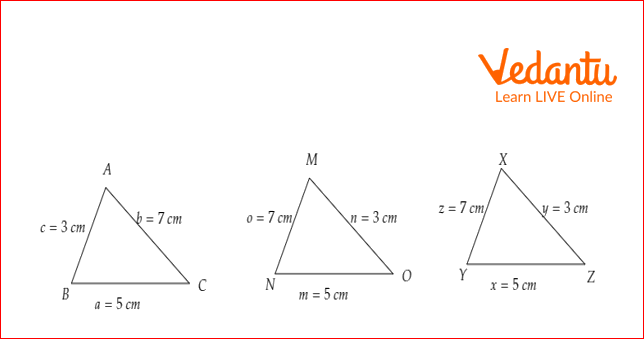
Example 3: If triangle ABC is congruent to triangle XYZ, the length of the sides of triangle XYZ is the same as the length of the sides of MNO. In other words, triangle ABC is congruent to triangle XYZ and triangle XYZ is congruent to triangle MNO. According to the transitive property, triangle ABC is congruent to triangle MNO.
Solved Examples
1. The weight of a dictionary is the same as the weight of a storybook. The magazine weighs the same as the weight of the storybook. If the weight of the magazine is 1.8 lb, what is the weight of the dictionary?
Solution: Let the weight of the dictionary, storybook, and magazine be \[w_d\], \[w_s\], and \[w_m\], respectively.
The weight of the dictionary and storybook are the same.
\[w_d=w_s\] …..(1)
The magazine's weight is equal to the weight of the storybook.
\[w_m= w_s\]
\[1.8 = w_s\] ....(2)
From equation 1, we have\[w_{d}=w_{s }= 1.8 \] lb
Therefore, the weight of the dictionary = 1.8 lb.
2. Susanne is given the information that line p II line q and line q II r. She wants to know the relation between angles a and b. Can you help her find the answer?
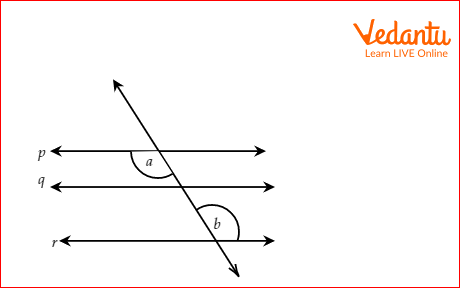
Solution: Since, line p II line q and line q II line r, therefore, by the transitive property of equality, line p II r.
We know that when two lines are parallel, the corresponding angles are equal. Here, a and b are alternate interior angles. Hence, they have equal measures.
Therefore, angle a = angle b.
3. The number of interior angles of polygon A is equal to the number of interior angles of polygon B. Polygon A is a pentagon. Again, the number of interior angles of polygon C is the same as the number of interior angles of polygon B. What is the number of interior angles of polygon C?
Solution:
The interior angle of a pentagon is 5.
The number of interior angles of polygon A =5
The number of interior angles of polygon A = number of interior angles of polygon B.
The number of interior angles of polygon B = number of interior angles of polygon C.
According to the transitive property, the number of interior angles of polygon A = number of interior angles of polygon C = 5.
Key Features
If a, b, and c are three quantities such that a is related to b by some rule and b is related to c by the same rule, then a and c are related by the same rule.
For the application of transitive property, we require three quantities.
Transitive property can be applied to real numbers, angles, lines, and triangles.
Practice Problem
1. If a = b = 8.43 and the value of c is the same as b, then find the value of c.
Answer: c = 8.43
FAQs on Transitive Property in Maths Explained
1. Is transitive property applicable to divisibility?
Let a = 12, b = 6, and c = 3. a is divisible by b, and b is divisible by c. We know that 12 is also divisible by 3. Thus, a is divisible by c. Hence, the transitive property is applicable to divisibility.
2. Is transitive property applicable to multiples?
Assume that x, y, and z are three numbers such that x is a multiple of y and y is a multiple of z. Since x is a multiple of y, thus x = ky. Since y is a multiple of z, thus y = mz. Now putting y = mz in x = ky, x = kmz.
So, x is a multiple of z. This satisfies the transitive property.
3. If point A and point B lie in the first quadrant and point C lies in the same quadrant where point B lies. Does it follow transitive property?
Since point B lies in the first quadrant, point C lies in the first quadrant. Thus, point A and point C lie in the first quadrant. Thus, it follows transitive property.
























