Introduction to Angles of a Quadrilateral
Sum of the angles of the quadrilateral is \[\left( {n - 2} \right) \times 180^\circ \], the formula for the interior angle sum of a quadrilateral, where n is the number of sides of the provided polygon. 180° - interior angle is the exterior angle. When a quadrilateral's inner angle is known and the value of the matching exterior angle is needed, this formula is utilized.
Definition of a Quadrilateral
A closed quadrilateral has four sides, four vertices, and four angles. It is a form of a polygon. In order to create it, four non-collinear points are joined. Quadrilaterals always have a total internal angle of 360 degrees.
Three Angles of a Quadrilateral Sum
Four-sided polygons with four vertices and four internal angles are known as quadrilaterals. Quadrilaterals come in a variety of shapes, including squares, rectangles, rhombus, and others. Because the internal angles of a quadrilateral always add up to \[360^\circ \], the unknown angles of a quadrilateral can be simply determined if the other angles are known.
Quadrilateral Angles Formula
The number of triangles that can be produced in a polygon can be used to determine the interior angle sum, in accordance with the polygon's angle sum attribute. By tracing diagonal lines from a single vertex, these triangles are created. This can be determined using a formula that states that if a polygon has 'n' sides, it will contain \[\left( {n - 2} \right)\] triangles.
\[S = [n - 2] \times 180\] is a formula that can be used to compute the sum of interior angles in a polygon, where n is the number of sides in the supplied polygon.
When we apply the formula to a quadrilateral, for instance, we get the following results: \[S = [n - 2] \times 180^\circ ,S = [4 - 2] \times 180^\circ = 360^\circ \]. The sum of a quadrilateral's internal angles is therefore always 360 degrees, according to the quadrilateral's angle sum condition. This characteristic aids in determining a quadrilateral's unknown angles. The value of the unknown angle can be determined by subtracting the sum of the other angles from \[360^\circ \] if the other angles are known.
Interior Angle of a Quadrilateral
Its internal angles are the angles that make up a quadrilateral. A quadrilateral's internal angles add up to 360°. This aids in figuring out a quadrilateral's unknown angles. We know that all of the quadrilateral's inner angles are 90 degrees each if it is a square or rectangle.
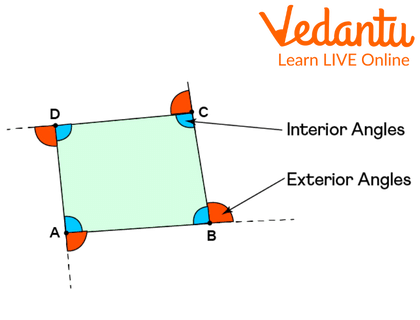
Exterior Angle of a Quadrilateral
The external angles of a quadrilateral are those that are created between a side and a line that extends from a neighboring side. If we look at the above illustration, we can see that the outer and interior angles combine to form a straight line, which is why they form a linear pair.
Quadrilateral Angle Calculator
Conclusion
The sum of the internal angles of a quadrilateral is 360 degrees. Quadrilaterals are four-sided polygons that have four internal angles and four vertices. Numerous shapes, such as squares, rectangles, and rhombi, can be used to create quadrilaterals.
Solved Examples
Example 1: Find the fourth internal angle of a quadrilateral if the first three are provided as \[77^\circ ,98^\circ and110^\circ \].
Ans: The following formula can be used to get the quadrilateral's fourth angle:
360 - (Sum of the other 3 inner angles) (Sum of the other 3 interior angles)
Fourth angle unknown = 360 - (Sum of the other 3 interior angles)
Unknown fourth angle equals \[360^\circ - \left( {77 + 98 + 110} \right)\]
Fourth angle: \[360^\circ - \left( {77 + 98 + 110} \right] = 75^\circ \]
Example 2: If the inner angle of a quadrilateral is 68°, what is the external angle?
Ans: We are aware that a quadrilateral's interior and exterior angles form a linear pair. We will find the answer via the quadrilateral exterior angle formula.
\[180 - 68 = 112^\circ \] is the outside angle. The external angle is \[112^\circ \] as a result.
Example 3: Find the Missing Angle of a Quadrilateral:
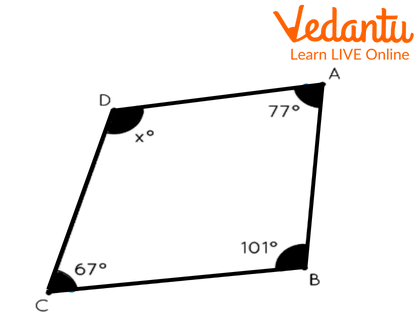
Ans: Applying Angle Sum Property in Quadrilateral we will get:
\[\begin{array}{l}x + 77 + 67 + 101 = 360\\x + 245 = 360\\x = 115\end{array}\]
FAQs on Three Angles of a Quadrilateral
1. A quadrilateral may have three angles.
We are aware that the sum of the angles of any quadrilateral must be 360 degrees. A quadrilateral cannot have three obtuse angles because this total cannot be both greater than 360° and equal to 360°.
2. What shape precisely has three angles?
A shape with three sides and three angles is a genuine triangle.
3. What are quadrilateral angles?
The four angles that are present at each vertex of a four-sided object are referred to as the inner angles of a quadrilateral and make up a quadrilateral.
