What Is the Tenth Decimal Place with Definition and Solved Examples
Decimals have always been a difficult topic for students. A decimal number comprises a whole number, and a fractional part that is separated by a dot called the decimal point. For example, 5.37 is a decimal number 5 is the whole number part, and .37 is the fractional part. The tenth decimal place, or decimal point, is the digit immediately to the right of the decimal separator with a value of 0.1. For example, if you have a number with one decimal place - such as 2.1 - then the tenth decimal place would be 1. The remaining ones continue to fill in the place values until there are no digits.
Tenth Decimal Place
The "deci-" prefix, as in "decimeter," denotes the tenth place. A decimeter is one-tenth of a meter. Now the question arises where is the tenth place in a decimal? According to the place value chart, the tenth place is situated between the decimal point and the hundredth place.
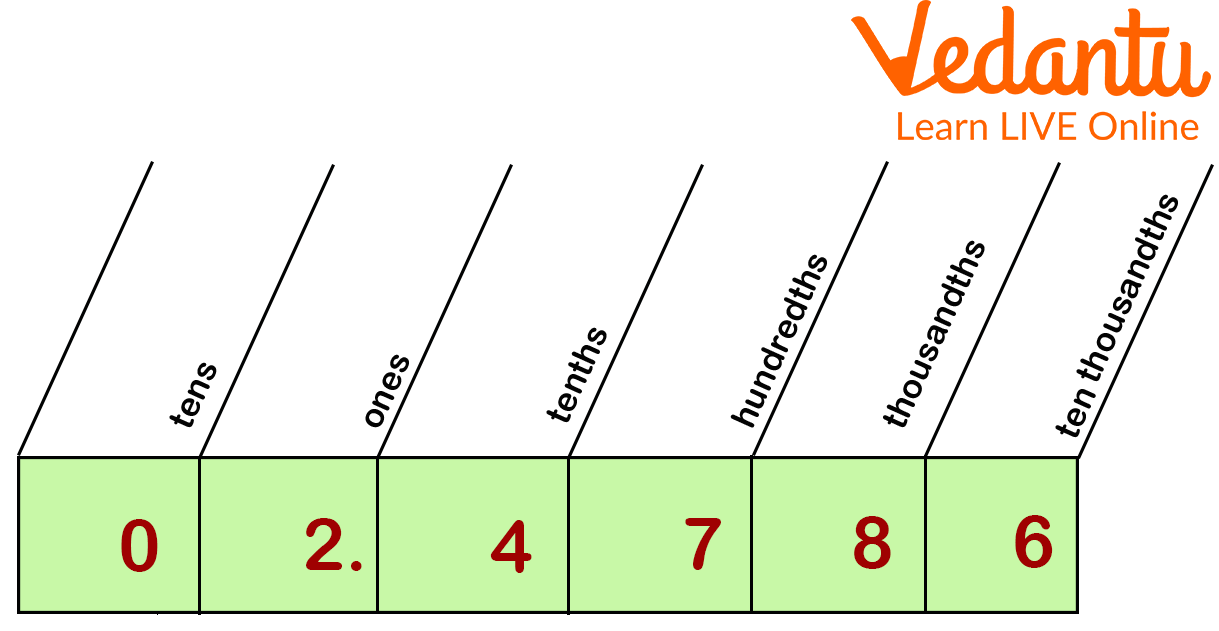
Place Value
Visualization of Tenth Decimal Place
Using base 10 blocks is useful for visualizing decimals. Consider a huge square representing one whole, for example. Each of the 10 equal-sized strips created from the square symbolizes one-tenth, or 0.1. To represent hundredths, each strip can be divided into 10 smaller squares.
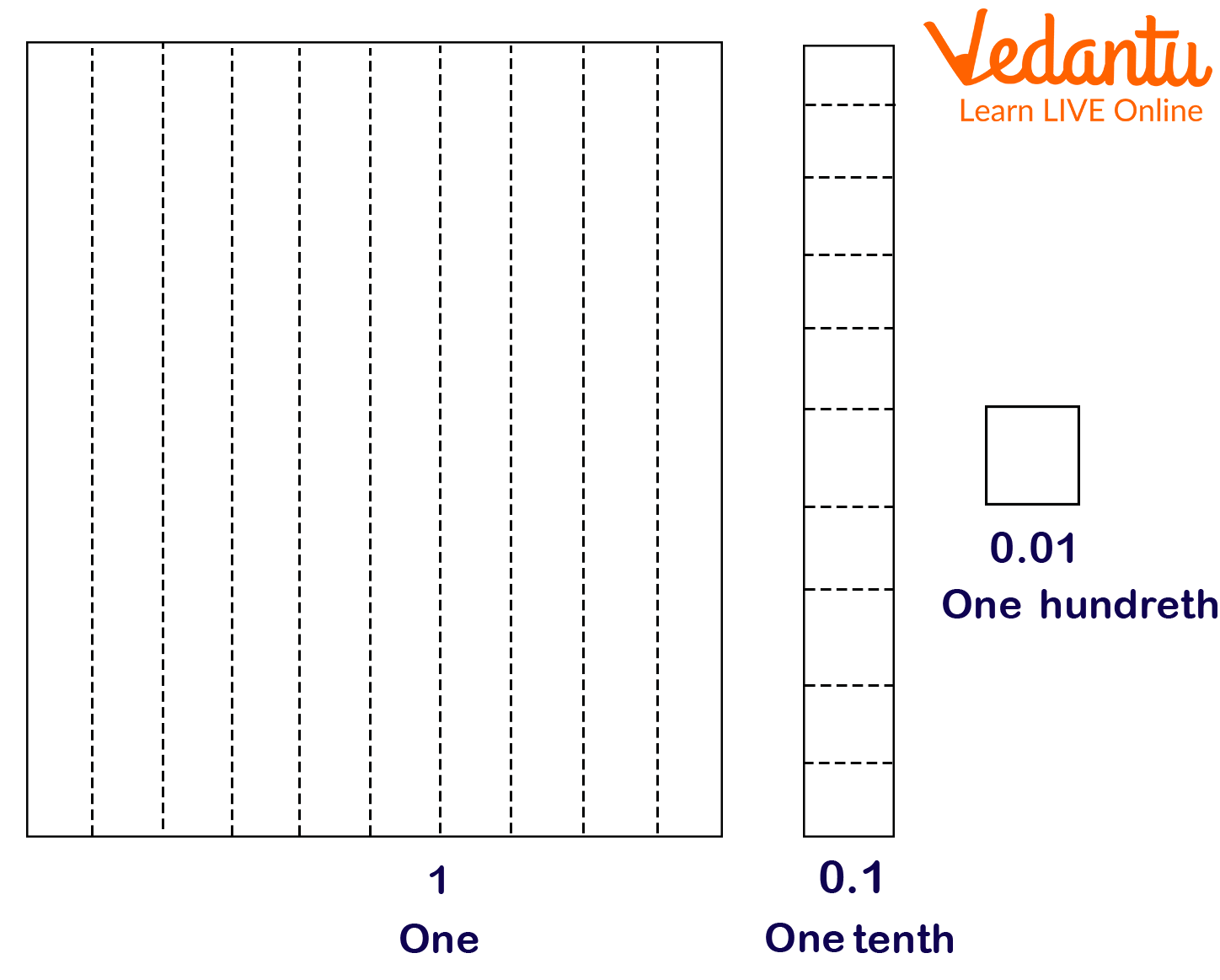
Visualisation of Tenth Decimal Place
What is the Tenth Place in a Decimal?
In a decimal number, as we move to the left, taking decimal as a reference point, each position is 10 times bigger. If we move to the right from the decimal point, each position is 10 times smaller. For example In, the number 396.7
The "6" is in the One's position, meaning 6 ones (which is 6).
The "9" is in the Tens position meaning 9 tens which are ninety.
And the "3" is in the Hundreds position, meaning 3 hundred.
This is when we move left from the decimal point; when we move right to the decimal point, each position is 10 times smaller, and tenths are $\dfrac{1}{10}$. For example, 396.7; the number will be read as three hundred ninety-six and seven-tenths, but we usually read it as three hundred ninety-six point seven.
Let’s explore where is Tenth Place in a decimal. The placement (or "place") of each digit in a number is crucial. The digit following the decimal point should be read with the word "tenths" in place of the decimal point. The alternative reading strategy is to just read the decimal point as a "point" before reading each individual digit as a word.
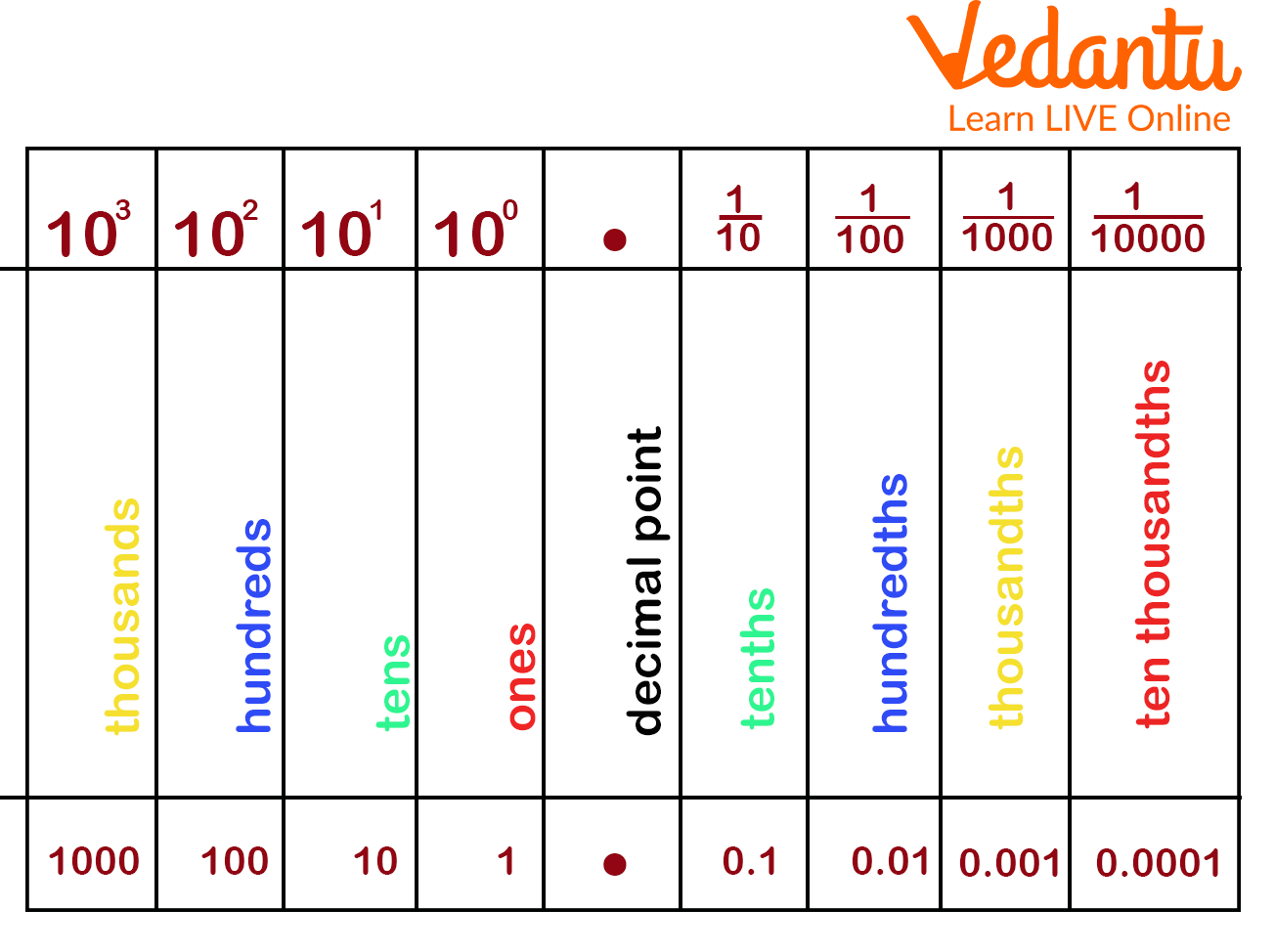
Location of Tenth Place in Decimal
The tenth place, as well as the adjacent place values, are displayed in red. Any digit that is in the tenth place has a value of 0.1, which is the result of the digit and $\dfrac{1}{10}$. For instance, the digit in the tenth place in the number 5.62 is 6, and its value is $0.1 \times 6 = 0.6$, or $\dfrac{6}{10}$.
Tenth Decimal Place Examples
let's have an example:
Here is the decimal representation of the number "forty-five and six-tenths":
Between Ones and Tenths, the decimal point is located.
Tenth Decimal Place
4 Tens, 5 Ones, and 6 Tenths make up the number 45.6 as follows:
$45.6 = 40+5+\dfrac{6}{10}$
Solved Examples
Q1. What is the sum of the digits at the tenth and hundredth places in the number 344.768?
Ans: Here, the digit at the tenth place = 7
The digit at the hundredths place = 6
Therefore, the Sum of digits= 7+6 = 13.
Q2. What number appears in the tenth place in 93.347?
Ans: The first digit following the decimal point is represented by the tenth place.
The second digit following the decimal point in 93.347 is 3.
Q3. What is 2.3?
Ans: The entire number portion, "2," is located on the left.
The number three is in the "tenths" position, which is "3 tenths," or $\dfrac{3}{10}$.
2.3 is, therefore, "2 and 3 tenths."
Practice Problems
Q1. Find the tenth-place value in 8.364. (Ans: 3)
Q2. Find the tenth-place value in 1058.56. (Ans: 5)
Summary
Decimals provide a convenient shorthand for fractions and mixed numbers with denominators that are powers of 10, such as 10,100,1000,10000, etc. The first digit represents the tenth place following the decimal. If a number has one, the first digit to the right of the decimal point represents the number of tenths. The second digit represents the number of hundredths to the right of the decimal point. For instance, the fractions $\dfrac{3}{10}$ and the decimal 0.3 are equivalents.
FAQs on Tenth Decimal Place in Decimal Numbers
1. What is the tenth decimal place?
The tenth decimal place is the digit located ten places to the right of the decimal point in a number. In a decimal number like 0.1234567895…, the tenth decimal place is the tenth digit after the decimal point. Decimal places are counted starting from:
- 1st – tenths
- 2nd – hundredths
- 3rd – thousandths ...
- 10th – ten-billionths (10⁻¹⁰)
2. What is the value of the tenth decimal place?
The value of the tenth decimal place is 10⁻¹⁰, which equals 0.0000000001. Each decimal place is 10 times smaller than the one before it. For example:
- 1st decimal place = 10⁻¹ (0.1)
- 5th decimal place = 10⁻⁵ (0.00001)
- 10th decimal place = 10⁻¹⁰
3. How do you find the tenth decimal place in a number?
To find the tenth decimal place, count ten digits to the right of the decimal point. Follow these steps:
- Step 1: Locate the decimal point.
- Step 2: Count digits moving right.
- Step 3: The 10th digit is the tenth decimal place.
4. What is an example of a number rounded to the tenth decimal place?
A number rounded to the tenth decimal place keeps ten digits after the decimal point. Example: Round 2.718281828459 to ten decimal places.
- Look at the 11th digit (which is 5).
- Since it is 5 or more, increase the 10th digit by 1.
5. Why is the tenth decimal place important?
The tenth decimal place is important in fields that require high precision, such as science, engineering, and finance. Very small differences can matter in:
- Scientific measurements
- Computer calculations
- Statistical data analysis
6. What comes after the tenth decimal place?
The place after the tenth decimal place is the eleventh decimal place, which represents 10⁻¹¹. Decimal places continue infinitely in theory. For example:
- 10th decimal place = 10⁻¹⁰
- 11th decimal place = 10⁻¹¹
- 12th decimal place = 10⁻¹²
7. How do you round a number to the tenth decimal place?
To round to the tenth decimal place, look at the digit in the eleventh decimal place. Follow these steps:
- If the 11th digit is 5 or more, add 1 to the 10th digit.
- If the 11th digit is less than 5, keep the 10th digit the same.
- Remove all digits after the 10th place.
8. Is the tenth decimal place the same as ten decimal places?
Yes, the tenth decimal place refers to the tenth digit after the decimal point, meaning the number is written to ten decimal places. For example, 0.1234567890 has exactly ten decimal places, and the digit 0 is in the tenth decimal place.
9. How do trailing zeros affect the tenth decimal place?
Trailing zeros can occupy the tenth decimal place without changing the number’s value. For example, 0.5 can be written as 0.5000000000 to show ten decimal places. The value remains 0.5, but the precision is expressed to the tenth decimal place.
10. What is the difference between the tenth decimal place and the tenth place value?
The tenth decimal place refers to the tenth digit after the decimal point, while the tenth place value usually means the tens place to the left of the decimal. For example, in 42.1234567895:
- 4 is in the tens place (10¹).
- 5 is in the tenth decimal place (10⁻¹⁰).
