Subtraction of Complex Numbers

In everyday life, addition and subtraction are the most used mathematical operations. We use it on a daily basis. If we go to the supermarket for shopping, we need an addition or subtraction of money to make the payment. We use addition or subtraction when we have some chocolates, and someone gives us more chocolates or if someone takes some chocolates from us.

Confused about complex numbers? Don't worry; all your doubts will be cleared after reading this article. Because in this article today, we are going to learn about what complex numbers are, what their properties are when it comes to subtraction, and what the steps are to solve complex numbers. So now, let's learn about the subtraction of complex numbers.

What are Complex Numbers?

Complex numbers are also numbers, but they are different from normal numbers in many ways. They are made with the help of two numbers that are combined.

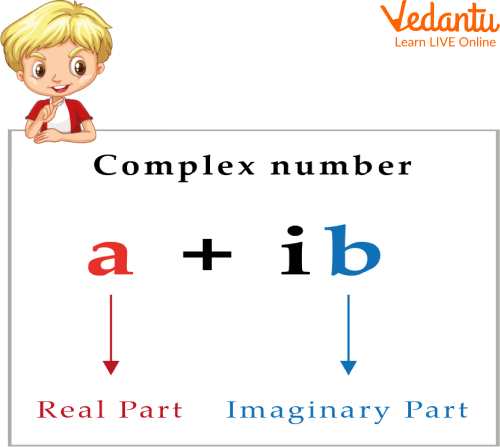
And in the new combined number, the first number is the real number, and another one is the imaginary number. Like all complex numbers can be expressed in the form a + bi, here, a is the real number, and bi is the imaginary number.

Remember that Complex Numbers are denoted by the letter 'C'.

Complex numbers also use all mathematical operations: addition, subtraction, multiplication, and division. But today, we will learn about the subtraction of complex numbers, which is as easy as solving a normal number.

And the Subtraction of complex numbers requires a formula.

Do you know the formula for the subtraction of Complex Numbers?

So the formula is (a+ib) - (c + id) = (a-c) +i(b-d).

Complex Number

Properties of Subtracting Complex Numbers

1. Closure property - In the closure property of Subtracting Complex Numbers, the difference between complex numbers is also a complex number.

2. Commutative property- Subtraction of complex numbers is not commutative.

3. Associative property- Subtraction of complex numbers is not associative.

Remember that this general form of a complex number is different from the polar form. Similarly, the addition and subtraction of complex numbers in the polar form are different.

Steps to Subtract Complex Numbers

Subtraction of two complex numbers is easy if it's done in the right and systematic way. So let's see the steps of subtraction of complex numbers.

$\mathrm{z}_1=\mathrm{a}+\mathrm{ib}, \mathrm{z}_2=\mathrm{c}+\mathrm{id}$

Subtraction

$\mathrm{z}_1-\mathrm{z}_2+(a-c)-(c+i d)$

$\mathrm{z}_1-\mathrm{z}_2=(a-c)+(b-d) i$

where $a, b, c, d$ are real number and $i$ is imaginary number

Step 1: Disperse the negative

Step 2: Now combine the real and imaginary complex numbers in a single group.

Step 3: Now, you need to combine and simplify similar terms.

Step 4: The answer will be there.

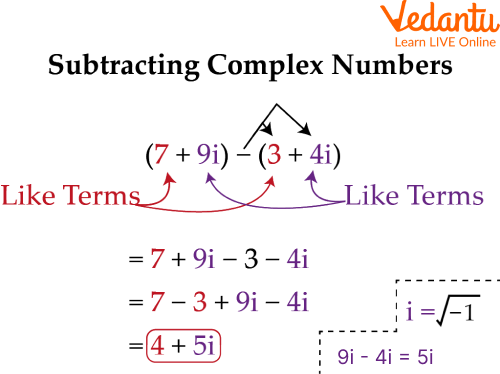
Subtraction of two complex numbers example

Subtraction of Complex Numbers Examples

For the subtraction of two complex numbers, we need to Subtract the real number from the real and the imaginary numbers from the imaginary. Let's learn it through examples:

Q 1. Subtract $(4-3 i)$ from $(7+5 i)$

Ans. $=7+5 i-(4-3 i)$

$=7+5 i-4+3 i$

$=3+8 i$

Q 2. Subtract ( 8 - 15i ) from (15 - 34i )

Ans. $=15-34 i-(8-15 i)$

$=15-34 i-8+15 i$

$=7-19 i$

Q 3. Subtract $(2+2 i)$ from $(3+5 i)$

Ans. $=3+5 i-(2+2 i)$

$=1+3 i$

Points to remember for the Subtraction of Complex Numbers

• Subtracting a complex number is like subtracting two binomials; we just need to combine the like terms.

• The subtraction of two complex numbers does not hold in the commutative law.

• All real numbers are complex numbers, but all complex numbers need not be real numbers.

Practice Questions

We know that maths is not learned just with reading. To understand it, we need to solve the question. So that's why we have provided a practice sheet for you. With the help of this practice sheet, you can better understand the subtraction of two complex numbers. Below are the addition and subtraction of complex numbers worksheets for your practice. Use the subtraction of complex numbers formula mentioned in this article to solve these problems.

Q1. $(16+5 i)+(8-3 i)$

Ans. $24+2 i$

Q2. $(5+7 i)-2 i$

Ans. $5+5 i$

Q3. $(4+3 i)-(4-3 i)$

Ans. 6i

Summary

In this article, we learned about the subtraction of complex numbers. With the help of this article, we learned what complex number is, how to subtract complex numbers, and what the properties of Subtracting Complex Numbers are.

We learn the steps we need to follow while subtracting a complex number. We also checked an example of subtraction of complex numbers, and at the end, there is a complex number worksheet with the help of which we can easily clear our concept of subtraction of complex numbers.