Properties of Division: Essential Concepts and Examples

The division is an arithmetic operation. An arithmetic operation combines two or more numbers using symbols known as arithmetic operators to form the resulting numeric expression. Division can be simply understood as splitting of equal groups of numbers and this rule known as the divide rule in maths. This article is about properties of division. There are many properties of division in mathematics, and this article will talk about them and what they mean. Division can seem like a complicated concept at first, but with an understanding of properties of division of integers, you'll find it much easier!

Division

Divide Rule in Maths

The division is a series of repetitive subtraction done to break down the larger number into smaller numbers, which when multiplied will be equal to the larger number. It is the inverse of the multiplication operation. There are 4 parts of division- The remainder, The Quotient, The Divisor, The Dividend.

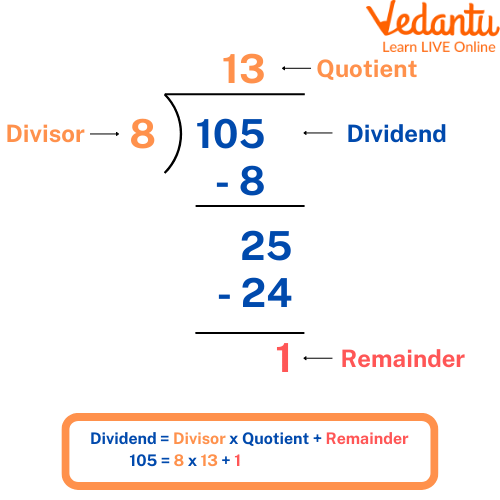
Division

The formula to calculate the division of two numbers is: Dividend ÷ Divisor = Quotient + Remainder. Here, The dividend is the number, which is being divided. The divisor is the number, which divides the number (dividend) into equal parts.

What are the Properties of Division?

In mathematics, a property is any characteristic that applies to a given set.

Following are the properties of division of integers:

• Property 1: The division of two nonzero integers $a$ and $b$, expressed as $a \div b$ is not necessarily a whole number.

• Verification: $a \div b$ gives a quotient that is a whole number $(c)$, then $a=b\times c$. However, in division operations such as $15 \div 2$ there exist no whole numbers whose product with 2 is 15 . Thus, $15 \div 2$ is not a whole number.

• Property 2: If a is a nonzero integer, then a divided by the number 1 then the quotient is a.

• $a \div 1=a$

Verification: let us take an example

Let $a=5$

$\therefore 5 \div 1=5$

The reason for this is that $5 \times 1=5$

• Property 3: If a nonzero number a is divided by itself, the quotient is 1.

• $a \div a=1$

Verification: Let's take an example of $3 \div 3=1$ Since $3 \times 1=3\quad \therefore 3 \div 3=1$

• Property 4: When 0 is divided by a nonzero number (a), the quotient is 0.

• $0 \div a=0$

Verification: Let us assume a=3

$3 \times 0=0 \quad \therefore 0 \div 3=0$

• Property 5: If $a, b$, and $c$ are nonzero whole numbers then if $b \times c=a, a \div c=b$, and $a \div b=c$

• Verification: Let us take an example

$3 \times 4=12$

$\therefore 12 \div 3=4 \text { and } 12 \div 4=3$

• Property 6: Any number divided by 0 is not defined.

• $a \div 0$ = not defined.

• Verification - Since no number can be divided by 0 to give a valid quotient the answer of this operation is termed as not defined.

• Property 7: The Division Algorithm

• The division Algorithm states that if a nonzero whole number a (dividend) is divided by a nonzero number b (divisor) then there is a whole number q (quotient) and r (remainder) such that a= bq + r , wherein r = 0 or r < b

Tips and Tricks

• When a 2- digit number is divided by 10 then the number in the tens place becomes the Quotient and the number in the one place becomes the remainder

• Eg. 32 ÷ 10. Here the quotient is 3 and the remainder is 2

• When a number is divided by 100 then the numbers hundreds place becomes the Quotient and the numbers in the ones and tens place become the remainder.

• You can check whether your division is correct by applying the division algorithm.

Solved Examples

Q1. Fill in the blanks:

1. 12 ÷ 1 =?

Ans: 12

Explanation- any number divided by 1 gives a quotient equal to the integer itself.

2. 31 ÷ 31=?

Ans: 1

Explanation - any number divided by itself gives the quotient 1.

Q2. State whether the statement is true or false: Zero divided by 6 gives the quotient 0.

Ans: True as zero divided by any nonzero integer is equal to 0.

Practice Problems

Q1. Fill in the blanks

1. 16 ÷ 16 =?

2. 0 ÷ ? = 0

Ans: 1. 16 ÷ 16 = 1

2. Any number

Q2. Choose the correct option; What is the division algorithm

1. Divisor + Remainder = dividend and quotient

2. Dividend = Divisor x Quotient + Remainder

3. Remainder = Dividend x Divisor + Quotient

Ans: 2. Dividend = Divisor x Quotient + Remainder

Summary

In this article, we will be discussing the properties of division of integers. Specifically, we will be looking at the divide rule in maths, what are the properties of division of integers, and examples. As we have seen that the division of two nonzero integers is not necessarily a whole number, if a nonzero integer is divided by 1 then the quotient is the dividend. If a nonzero number is divided by itself the quotient is 1. The quotient of any number divided by 0 is not defined. 0 divided by any number is equal to 0. If a, b, and c are nonzero whole numbers then if $\mathrm{b} \times \mathrm{c}=\mathrm{a}, \mathrm{a} \div \mathrm{c}=\mathrm{b} \text {, and } \mathrm{a} \div \mathrm{b}=\mathrm{c}$. If a nonzero whole number a (dividend) is divided by a nonzero number b (divisor) then there is a whole number q (quotient) and r (remainder) such that a= bq + r , wherein r = 0 or r < b. These are the properties we have learned. We hope that this article was helpful and that you now have a better understanding of what division is and how it works.