How to Add and Subtract Powers: Rules, Methods & Practice
Algebra is one of the very important parts of mathematics. To understand algebra, one must know how to use exponents and radicals. The power over the given base number is known as exponents/index. For example, $4^2=4 \times 4$, where 4 is the base and 2 is the exponent. The Addition of powers is the process of adding exponents or powers of a number irrespective of whether the base is the same. In this article, we will learn about the addition and subtraction of powers with numerical bases.
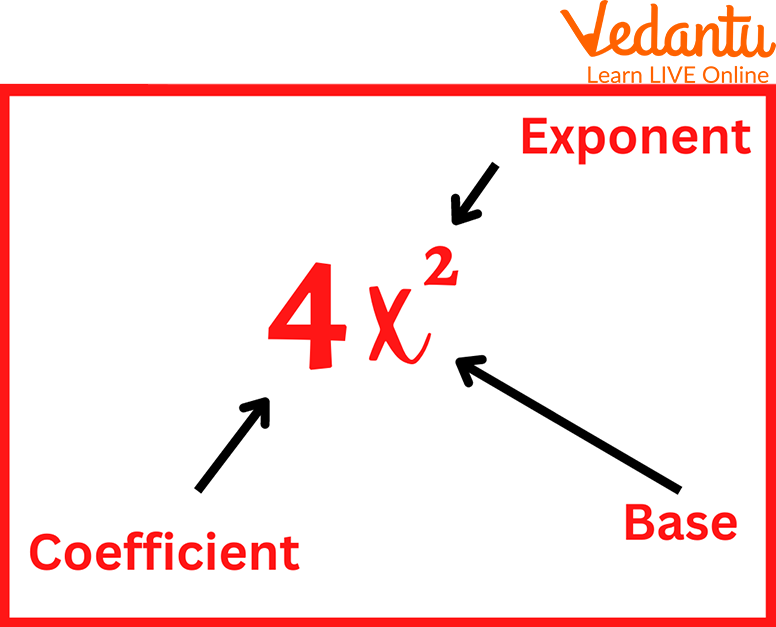
Introduction to Powers
Addition and Subtraction of Powers with Numerical Bases
Addition and subtraction are the two primary operations of mathematics. But we cannot directly add or subtract powers, we can only perform addition or subtraction only on the variables that have the same base and the same power. We can only add powers in multiplication and subtract powers in the division.
$3^4+2^5=$
$=3^4$
$=3 \times 3 \times 3 \times 3$
$=81$
Also, $2^5$
$=2 \times 2 \times 2 \times 2 \times 2$
$=32$
Therefore, $3^4+2^5= 81 + 32$
$=113$
Addition of Numbers with Powers
Adding numbers with power can be done when the base and powers are the same. There would be times when the base and powers are different, but we can still add those expressions. Let us have a look at the ways of adding powers.
Check if they got the same base and also the same power.
The usual form of addition of powers with same base is $x^{n}+x^{n}=2x^{n}$.
For example, $4^{2}+4^{2}$
$=2(4^{2})=2 \times 4 \times 4$
$=32$
If the base and power differ, then the expression will be calculated with individual terms.
The usual form is like $z^{n}+x^{m}$.
Addition and Subtraction of Powers
To add and subtract powers, you must first ensure that the base and power of the two terms we use to add or subtract are the same. If they are the same, then you only have to add together their coefficients and let the base and power remain identical.
$3^3+2^5 =?$
$=(3 \times 3 \times 3 )(2 \times 2 \times 2 \times 2 \times 2)$
$=(27)+(32)$
$=59$
$3^3+2^5=59$
Laws of Indices
The First Law: Multiplication
If the two terms have identical bases (in this case, " $\mathrm{x}$ ") and are to be multiplied, their indices will be added.
Let’s see the addition of indices with different powers, $x^m \times x^n=x^{m+n}$
Example: $5^2 \times 5^1=5^{2+1}=5^3$
The Second Law is: Division
If the two terms have an identical base (in this case, " $\mathrm{x}$ ") and are to be divided, their indices will be subtracted.
$\dfrac{x^m}{x^n}=x^{m-n}$
Example: $\dfrac{2^3}{2^2}=2^{3-2} =2^{1} = 2$
The third law: Brackets
If a term with an exponent is raised to a power, then the powers are multiplied.
$\left(x^m\right)^n=x^{m \times n}$
Example: $\left(3^2\right)^2=3^{2 \times 2}=3^{4}$
Solved Examples
Q 1. Find the value of $9^5$.
Ans: $9^5=9 \times 9 \times 9 \times 9 \times 9= 59,049$
Q 2. Find the value of $81+2^4=?$
Ans: $2^4$
$=2 \times 2 \times 2 \times 2 $
$=16$
Therefore, 81 + 16 = 97.
Q 3. Find the value of $2^6+3^5$
Ans: Since $2^6+3^5$ can be written in expanded form ad
$=(2 \times 2 \times 2 \times 2 \times 2 \times 2 )+(3 \times 3 \times 3 \times 3 \times 3)$
$=(64)+(243)$
$=307$
Practice Questions
Q 1. $\left(2^3\right)^2=$? (Ans: $64 .$)
Q 2. Find the value of $4^{-5}$. (Ans: $=\dfrac{1}{1024}$)
Q 3. $8^2 \times 4^1=$? (Ans: 256)
Summary
In this article, we have learned about the addition of power. Adding exponents refers to the simple addition of numbers but in the form of exponents or power. This article taught us that the variables and exponents must be the same to add or subtract with powers. The power of a number tells us how many times a number is to be used in multiplication. Powers are also known as Indices or Exponents. For example, $7^{2}$ could be called “7 to the power of 2” “7’’to the second power”, or simply “7 squared”. In the end, we added the practice problem to check the command over the topic. So after going through the article, give it a try!
FAQs on Addition and Subtraction of Powers Explained
1. What is the main rule for adding and subtracting terms with powers?
The fundamental rule is that you can only add or subtract like terms. For terms with powers, this means they must have both the same base and the same exponent. When these conditions are met, you simply add or subtract their coefficients and keep the base and exponent the same. For example, 3x² and 5x² are like terms, so their sum is 8x².
2. Can you provide some examples of adding and subtracting powers?
Certainly. Here are some examples that illustrate the rule for like terms:
Addition Example (Like Terms): To solve 4a³ + 6a³, you add the coefficients (4 + 6) to get 10, keeping the base and exponent the same. The answer is 10a³.
Subtraction Example (Like Terms): To solve 9y⁵ - 2y⁵, you subtract the coefficients (9 - 2) to get 7. The answer is 7y⁵.
Unlike Terms Example: The expression 5x² + 3x⁴ cannot be simplified further because the exponents (2 and 4) are different, making them unlike terms.
3. What happens when you add or subtract terms with powers that have different bases?
You cannot combine or simplify terms that have different bases, even if their exponents are the same. For instance, in the expression x² + y², the bases 'x' and 'y' are different. Since they are not like terms, the expression cannot be simplified and must be left as is. This is a key difference from multiplication, where you can combine terms with different bases.
4. How is adding powers different from the rule for multiplying powers?
The rules are completely different and address separate operations:
Adding Powers: This involves combining like terms (same base and exponent) by adding their coefficients. For example, 2x³ + 3x³ = 5x³.
Multiplying Powers: This involves terms with the same base but not necessarily the same exponent. You add the exponents together. For example, x² ⋅ x³ = x⁽²⁺³⁾ = x⁵.
Confusing these two rules is a very common mistake.
5. Can you add powers if the bases are the same but the exponents are different, for example, a³ + a⁵?
No, you cannot directly combine a³ + a⁵ into a single power term like a⁸. Because the exponents are different (3 and 5), they are considered unlike terms. The expression a³ + a⁵ is its simplest form. The rule of adding exponents only applies when you are multiplying terms with the same base (a³ ⋅ a⁵ = a⁸), not when you are adding them.
6. What is the most common mistake students make when subtracting powers?
The most frequent error is incorrectly applying the exponent rule for division (where exponents are subtracted) to the subtraction of terms. For instance, a student might mistakenly calculate x⁵ - x² as x³. This is incorrect. The correct approach is to recognize that x⁵ and x² are unlike terms because their exponents differ. Therefore, the expression x⁵ - x² cannot be simplified further.
7. Why does the rule for zero exponents state that any non-zero number to the power of zero is 1?
This rule exists to maintain consistency with other laws of exponents, particularly the division rule. Consider the expression aᵐ / aᵐ. We know that any number divided by itself equals 1. Using the exponent division rule (aᵐ / aⁿ = aᵐ⁻ⁿ), we get aᵐ / aᵐ = aᵐ⁻ᵐ = a⁰. Since both are true, it logically follows that a⁰ must equal 1. This ensures all the exponent rules work together harmoniously.
8. How do negative exponents relate to addition and subtraction of powers?
A negative exponent represents a reciprocal, for example, x⁻² = 1/x². When adding or subtracting, you must first convert the negative exponent into its positive fractional form. For example, to solve 3x⁻² + 5x⁻², you would treat it as 3(1/x²) + 5(1/x²). Since they are like terms, you can add them to get 8(1/x²), which is 8x⁻². The core rule of matching bases and exponents still applies.
