Identifying Patterns and Rules

Do you know what patterns are? Or how to identify them? What to do after identifying them? How are they helpful? Patterns can be anything that is repeated after some time, a design, number, formula, or even a rule. What are the rules? Rules are a set of words that guide you about a particular way of doing something. Today, we will discuss patterns and rules in Maths. We will also discuss how these patterns or rules can solve any problem. By the end of this, we will solve a few examples.

What is a Pattern in Maths?

Patterns in Maths are also called sequences, and these are sets of terms that contain a formula that repeats itself after some time.

Number Patterns

Number patterns are where numbers follow a certain formula and make a sequence from it. There are various types of number patterns, namely, Arithmetic, Geometric, and Fibonacci sequences.

Number Patterns Example

• Arithmetic Pattern

Also known as an algebraic pattern, a sequence is formed by adding or subtracting.

Example: 1, -1, -3, -5, -7, -9, and so on.

In the given example, 2 is subtracted from the preceding number, creating the sequence.

1 - 2 = -1

-1 - 2 = -3, etc.

• Geometric Pattern

These are formed by using multiplication or division

Example: 1, 2, 4, 8, 16, 32…

Here, we are multiplying 2 to get the next term of the sequence.

1 $\times$ 2 = 2

2 $\times$ 2 = 4, …

• Fibonacci Pattern

This is a sequence formed by adding the previous two terms of a sequence.
Example: 0, 1, 1, 2, 3, 5, 8, 13, and so on.

Here, we are adding the first two terms, then the next two, and so on.

0 + 1 = 1

1 + 1 = 2

1 + 2 = 3

2 + 3 = 5, and so on.

Types of Patterns

There are various types of sequences in Maths:

• Repeating Patterns

These patterns have rules that keep repeating after some time.

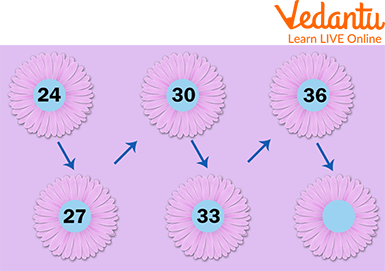
• Growing Patterns

These patterns keep growing, which means the value of terms keeps increasing.

Example: In the image given below, 2 is added to the previous number.

Growing Patterns

• Shrinking Patterns

These patterns keep shrinking or getting smaller, which means the value of terms keeps decreasing.

Example: In the image given below, 2 is subtracted from the preceding number.

Shrinking Pattern

Rules in Maths

Let’s see the definition of rules in maths. Every pattern has some kind of rule. These rules are used to find missing terms in a sequence, much like adding a number. When trying to understand the nature of the sequence, we use the difference between two consecutive terms to find the rule.

Let’s take an example: 1, 8, 27, 64, 125, etc.

Let the first term be $a_0$, the second be $a_1$, the third be $a_2$, and so on.

Now $a_0$ = 1, which is = 1$\times$1 = 1$\times$1$\times$1,

$a_1$ = 8, which is = 2$\times$2$\times$2,

$a_2$ = 27, which is 3$\times$3$\times$3.

Here, the nature of the sequence is geometric, as the number is the cube of the position of the number (The first number in the sequence is the cube of one, and the second is the cube of 2).

Solved Examples

Now that we have learned about patterns and rules, we will try to solve some examples of patterns and rules examples.

Q 1: Determine the P value in the sequence of numbers: 1, 4, 9, P, 25.

Ans: In the given sequence, the pattern that we see is that every number is the square of the counting numbers.

The square of 1 is 1, the square of 2 is 4, and so on.

Hence, the missing number 'P' is a square of 4, which is 16.

Example 2: Find the value of P and Q in 1, P, 9, Q, 25.

Ans: $1 = 1 \times 1$

$9 = 3 \times 3$

$25 = 5 \times 5$

This explains that a term's value in the given sequence depends on its position. If the position is n, then the term's value is $n^{2}$.

So, $P = 2 \times 2 = 4$ and $Q = 4 \times 4 = 16$.

Example 3: Determine the value of D in the sequence of numbers: 11, 17, 23, 29, D, 41, 47, 53

Ans: By adding the number 6 to the given sequence, we can see the pattern of every number increasing.

11 + 6 = 17, 17 + 6 = 23, and so on.

Hence, the missing number D is 29 + 6 = 35.

Try Some Yourself

Now that we have solved a few examples, let’s see if you can solve some on your own too.

Q 1. Find the value of A and B in 0, A, 8, 15, and B.

Ans: A = 3 and B = 24.

Hint: Subtract one from the square of the position of the term.

Q 2. Find the value of R and S in R, 2, 3, 4, S.

Ans: R = 1 and S = 5.

Q 3. Find the missing numbers in the pattern: 8, ______, 16, ______, 24, 28, 32.

Ans: 12, 20

Summary

Learning patterns improves our ability to spot patterns. We see a pattern that prompts us to think about and determine the rule that will allow the pattern to continue. We use rules to find terms missing from a given pattern. Rules can be found using the relation and difference between two consecutive numbers in a pattern. A pattern in maths is a set of numbers that relate to each other, forming a sequence. Number patterns can be of three types: Arithmetic, Geometric and Fibonacci patterns, while patterns have three types, namely, Repeating, Growing, and Shrinking. As the name suggests, repeating patterns have rules that repeat while the value of terms increases in Growing patterns and decreases in Shrinking patterns.