Numerator and Denominator in Fractions

We often speak of quantities as half, or one-third, or one-fifth, and so on. Well, these are “parts of a whole quantity”, and are represented as fractions, $\frac{1}{2}, \frac{1}{3}, \frac{1}{5}$. A fraction has two parts, numerator and denominator, separated by a horizontal line. The horizontal line is called the vinculum. The numerator refers to the part of the fraction above the vinculum and the denominator refers to the part of the fraction below the vinculum. For any given fraction, the denominator represents the whole quantity and the numerator represents a part of the whole quantity.

Examples of Fractions

Let us now understand the concept of numerator and denominator in a detailed manner, with the help of some examples.

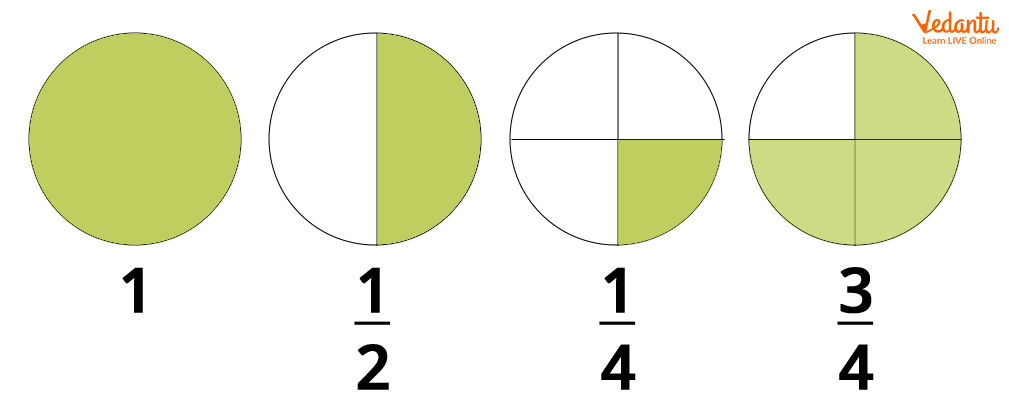
A Diagrammatic Representation of Fractions

In the figure above, a circle represents the total given quantity. The green parts of each circle represent the numerator of the respective fraction whereas the white parts represent the denominator. When the numerator and denominator are equal, that is, the number of green parts is equal to the number of white parts, the value of the fraction becomes 1.

Example of Pizza: Numerator and Denominator

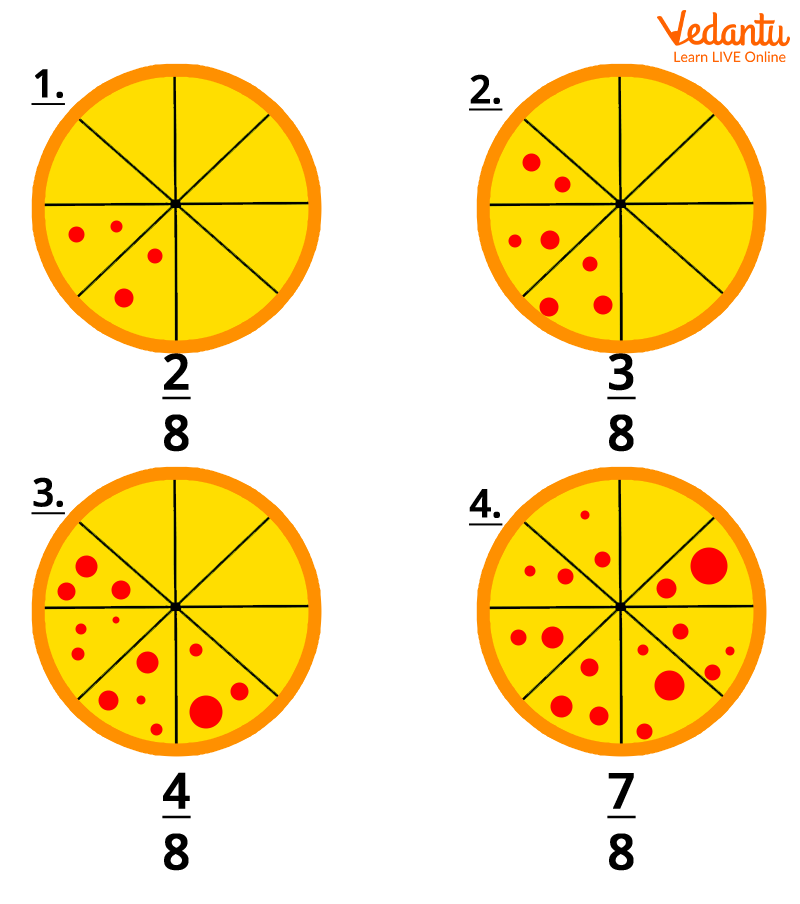
Pizza Example for Numerator and Denominator

Let’s assume you order a pizza for 8 of your friends, but when the pizza is delivered, you find that it is not cut into equal parts. Before sharing the pizza equally among all, you will have to divide the pizza into 8 equal parts. To determine the fraction of pizza each of your friends had, consider 8 as the denominator of the fraction, and the number of equal slices of the pizza one has will be the numerator. For example, the third circle has 4 in the numerator and 8 in the denominator. Therefore, 4 slices of pizza are considered out of the 8 slices for this fraction.

Solved Examples

I. Identify the numerator and denominator in the following fractions:

$\frac{3}{5}, \frac{23}{16}, \frac{27}{9}, \frac{2}{16}, \frac{24}{48}$

Solution:

The numerator and the denominator of the given fractions are as follows:

$\frac{3}{5}$

Numerator = 3, Denominator = 5

$\frac{23}{16}$

Numerator = 23, Denominator = 16

$\frac{27}{9}$

Reducing the fraction to its simplest form, we will divide the numerator and denominator by 9. We get

$\frac{3}{1}$

Therefore, numerator = 3, denominator = 1

$\frac{2}{16}$

Reducing the fraction to its simplest form, we will divide the numerator and denominator by 2. We get

$\frac{1}{8}$

Numerator = 1, Denominator = 8

$\frac{24}{48}$

Reducing the fraction to its simplest form, we will divide the numerator and denominator by 24. We get

$\frac{1}{2}$

Numerator = 1, Denominator = 2

Understanding the concept of numerator and denominator will help kids express various quantities in the form of fractions and analyse their value. With good practice, as soon as they see a fraction, they will be able to reduce its numerator and denominator fractions to the simplest form. There are several applications of fractions in subjects other than Mathematics. Therefore, the knowledge of numerator and denominator will enhance the analytical and problem-solving skills of kids for the other subjects as well.