Divisible of 4

You must have heard the word “divisibility” in Maths. The meaning of divisibility is the capacity to be completely divided without remainder. Some divisibility rules must be followed to check this divisibility. Without doing actual division, how can we guess numbers divisible by 4 or not? In this article, you will be learning the divisibles of 4 or the divisibility rules of 4. This article will explore the divisibility rule of 4 with examples and how it can be used to test whether a number is divisible by 4.

Divisibility Rule of 4

What Do You Mean by Divisibility?

Divisibility is defined as the rule or way to determine whether a given large or small number is divisible by a given fixed number (divisor).

A number is divisible by another number if it can be divided by that other number equally or if doing so results in a whole number. For instance, because 6 divided by 3 gives 2 and 2 is a whole number, then 6 is divisible by 3 (we say "3 divides 6").

A set of broad guidelines known as the "divisibility rules" is frequently used to determine whether or not a number is evenly divisible by another number. For e.g., if we have to check whether the number 432 is divisible by 4 or not.

Given number = 432

Fix number or divisor = 4

In detail, we will learn in the next heading about the numbers divisible by 4.

So for some numbers, we have some divisibility rule to find out whether the number is divisible by a divisor or not.

Division Into 4 Parts

Divisibility Rule of 4

The divisibility rule of 4 is defined as the given number being divisible by 4 if the last two digit numbers of the given number are zeros or they are the multiples of 4 (4, 8,12,16,20,24,.....).

This rule helps students to find out if the given number is divisible by 4 or not.

Some of the whole numbers which are divided by 4 completely are 0,4,8,12,16. We all know a table of 4. Hence these multiples of 4 are completely divisible by 4.

How to Check Divisibility by 4?

In this trick, we have to follow two conditions to check the divisibility test of 4 given as follows:

1. Check whether the last two digits of a given number are zeros. If yes, then the given number will be divisible by 4. If no, then check for the second condition given below. Zeros should be in the ones and tens place.
   
   

For e.g., 700 is a number that has zeros at ones and tens places. Hence, we can say that 700 is divided by 4 without doing any calculation.

2. Check if the last two digits of a given number are exactly the multiple of 4 or come in the table of 4, then we can say that the given number is divisible by 4.

For e.g., 736 checks two digit numbers are bold and underlined.

36 comes in the table of 4, or it is a multiple of 4. Hence we can say that 736 is completely divided by 4.

Divisibility Rule of 4 with Example

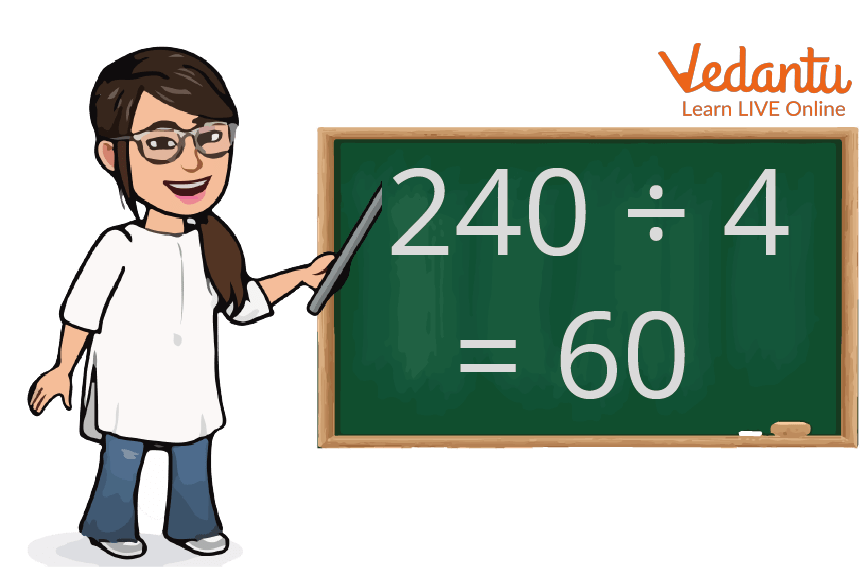
Some Examples

Here are some questions that show the numbers divisible by 4

1. Check whether the given numbers are divisible by 4 or not.

1. 1700

2. 6500

Ans:

1. 1700

Given the number- 1700

The last two digit numbers are -00

Hence Divisibility Rule 1 is followed, and 1700 is divisible by 4.

1700 ÷ 4 = 425

2. 6500

Given the number- 6500

The last two digit numbers are -00

Hence Divisibility Rule 1 is followed, and 6500 is divisible by 4.

6500 ÷ 4 = 1625

Practice Questions

Q 1. Which one of the following is completely divisible by 4? Tick the correct option.

1. 766

2. 222

3. 336

4. 811

Ans: 36

Q 2. Which one of the following is completely divisible by 4? Tick the correct option.

1. 555

2. 840

3. 114

4. 106

Ans: 840

Summary

Divisibility is defined as the rule or way to determine whether a given large or small number is divisible by a given fixed number (divisor). The divisibility rule of 4 is defined as the given number being divisible by 4 if the last two digit numbers of the given number are zeros or multiples of 4.