How to Multiply a Fraction with a Whole Number: Step-by-Step Guide

Multiply Fraction by a Whole Number in Just 2 Steps

Do you want to know what fractions and whole numbers are?

And!

How do fractions get multiplied by a whole number?

Here, we will discuss the two mathematical terms ‘Fractions’ and ‘Whole Number’ and how to multiply a fraction by a whole number in an easy way.

What Is a Fraction?

A fraction is nothing but a numerical value that represents a part of a whole unit.

Let us understand fractions with an example in a better way.

Slice a pizza, and you get a fraction.

Here,

The top number says how many slices you have.

The bottom number says how many equal sizes the whole pizza was split into.

Parts of A Fraction

A fraction has two parts, namely the numerator and the denominator.

The number written above the line is termed as the numerator. The numerator is the number of parts we have.

The number written below the line is termed as the denominator. The denominator is the number of parts the whole unit is split into.

The line that separates both the numerator and denominator is called a ‘Fraction Bar’ or ‘Vinculum’.

\[ \frac{Numerator}{Denominator} \]

Types of Fraction

Proper Fraction: A fraction whose numerator value is less than the denominator value is termed as proper fraction. For example, \[ \frac{2}{7} \], \[ \frac{3}{10} \],\[ \frac{1}{2} \], etc. are proper fractions.

Improper Fraction: A fraction whose numerator value is equal to or more than the denominator value is termed as improper fraction. For example, 5/2, 8/5, etc. are improper fractions.

Mixed Fraction: A fraction that is a combination of whole and a part is termed as a mixed fraction. For example,\[ 3\tfrac{1}{4} \] , \[ 2\tfrac{1}{2} \], etc. are mixed fractions.

What Are Whole Numbers?

In mathematics, whole numbers are simply numbers starting from 0. For example:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9,.... and so on

Remember!

Whole numbers do not include negative numbers, fractions and decimals.

Instead, whole numbers include only positive counting numbers.

How to Multiply a Fraction by a Whole Number in Two Steps?

The two steps to multiply a fraction by a whole number are as follows:

Step 1: Multiply the numerator values.

Step 2: Leave the denominator of the fraction the same.

Example:

Multiply \[ \frac{3}{2} \] x 5

Step 1: Multiplying the numerator values gives:

3 x 5 = 15

Step 2: Leaving the denominator of the fraction the same. Accordingly, the denominator will be 2.

Now:

The new numerator is 15.

The denominator 2 remains the same.

Hence,\[ \frac{3}{2} \] x 5 = \[ \frac{15}{2} \]

How to Multiply a Fraction by a Whole Number in Four Steps?

Step 1: Convert the whole number into a fraction with a denominator of 1. (We are doing this because anything divided by 1 remains the same).

Step 2: Multiply the numerators.

Step 3: Multiply the denominators.

Step 4: Simplify the fraction, if required.

Let us understand with an example:

Multiply \[ \frac{3}{2} \] by 8

Step 1: Convert the whole number into a fraction with a denominator of 1.

8 = \[ \frac{8}{1} \]

Step 2: Multiply the numerators.

3 8 = 24

Step 3: Multiply the denominators.

2 x 1 = 2

Hence,

The new fraction is \[ \frac{24}{2} \]

Step 4: Simplify the fraction:

\[ \frac{24}{2} \] = 12 or \[ \frac{12}{1} \]

How to Multiply a Mixed Fraction by a Whole Number?

The following are the steps to multiply a mixed fraction by a whole number:

Step 1: Convert the mixed fraction into an improper fraction.

Step a: Multiply the whole number by the improper fraction.

Note: To convert a mixed fraction into an improper fraction, multiply the whole number by the denominator and then add the result or product obtained by the numerator to get the new numerator value of the improper fraction. The denominator value of the improper fraction will be the same as it was before.

Example:

Multiply 3 x \[ 2\tfrac{5}{7} \]

Solution:

Step 1: Converting the mixed fraction into the improper fraction.

\[ 2\tfrac{5}{7} \]= \[ \frac{2 \times 7+5}{7} \]= \[ \frac{19}{7} \]

Step 2: Multiplying the improper fraction obtained in step 1 by the whole number.

\[ 3\frac{19}{7} \] = \[ \frac{19 \times 3}{7} \] = \[ \frac{57}{7} \]

Therefore, \[ 3 \times 2\tfrac{5}{7} \] = \[ \frac{57}{7} \] or \[ 8\tfrac{1}{7} \]

How Does Multiplying a Fraction by a Whole Number Work?

When a fraction gets multiplied by a whole number, it works as a repeated addition.

Let’s understand with an example:

Multiplying \[ \frac{5}{7} \] by 2 is the same as \[ \frac{5}{7} \] + \[ \frac{5}{7} \]

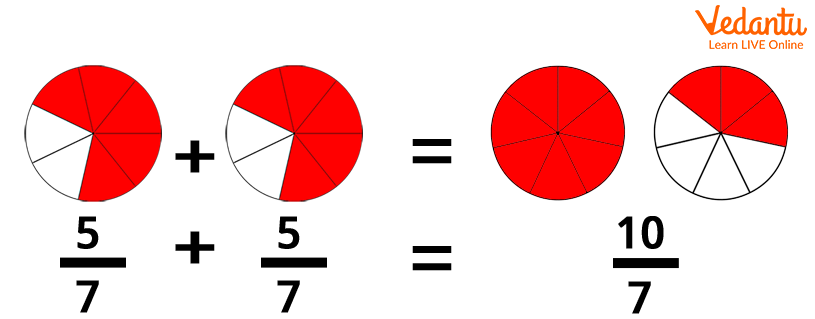
Remember! \[ \frac{5}{7} \] x2 = \[ \frac{5}{7} \] x \[ \frac{2}{1} \]= \[ \frac{5x2}{7x1} \] = \[ \frac{10}{7} \]

Hence, proved

Multiplication of Whole Number by Fraction Example Problem

Let’s say there are 10 oranges in the basket and \[ \frac{3}{5} \] of them are sour. How many oranges are sour?

Solution:

Finding \[ \frac{3}{5} \] by 10 is similar to \[ \frac{3}{5} \] x 10

Now, follow the above steps to multiply.

\[ \frac{3}{5} \] \times 10 = \[ \frac{3}{5} \] x \[ \frac{10}{1} \] = \[ \frac{3 \times 10}{5 \times 1} \] = \[ \frac{30}{5} \] = 6

Hence, 6 of the oranges are sour.

Did Any of You Know?

• The addition and multiplication of any two whole numbers can be done in any order.

• All numbers except 0 have an immediate predecessor or number that comes before.

• The decimal expansion of fraction either ends or keeps on repeating. For example, \[ \frac{1}{4} \] = 0.25, \[ \frac{1}{7} \] = 0.142857142857. On the other hand, the decimal expansion of irrational numbers nevers repeats.

Conclusion

In short, multiplying mixed numbers with whole numbers is a simple four step process. To convert, you just need to write the whole number as a fraction with a denominator equal to 1. Multiply both numerator and denominator values. Simplify the result if possible.