An Overview of Polynomials
In algebra, you may have studied variables such as x and y. Many expressions involve variables and constants. They are called polynomials. Polynomials are used in various fields such as science, technology, economics, social sciences, etc. These can be used to model a problem that occurs in nature, business, etc., as equations. These models can be used to find solutions to complex scientific problems. We can also classify polynomials based on the number of terms. We will discuss about different types of polynomials in this article.
What is Monomial?
A monomial is a type of polynomial that has only a single term. It can be a variable with a constant coefficient or only a constant. The term should not be zero. If a polynomial has only a constant, it is called a constant polynomial. A monomial should also have a non-negative degree, where the degree is the sum of exponents of variables in a term.
Examples of monomials are as follows:
\[5\]
\[3x\]
\[4y\]
\[16xy\]
\[2mn\]
What is Binomial?
A binomial is a polynomial that has only two non-zero terms related by addition or subtraction. A constant term can be present in a binomial. Examples of binomials are as follows:
\[x\, + \,3\]
\[3x\, + \,4\]
\[4xy\, + 3y\]
What is Trinomial?
A trinomial is a polynomial that has three terms related by addition or subtraction. All of its terms should not be zero. There can be a constant term in a trinomial.
Examples of trinomials are as follows:
\[3{x^2} + 4x + 9\]
\[6{x^2} + 3xy + 9{y^2}\]
What is Polynomial?
A polynomial is an expression consisting of variables and constants, related by addition or subtraction. It should have more than a single term. Examples of polynomials are as follows:
\[2{x^2} + 15x + 7\]
\[12{x^2} + 4x + y\]
Terms of a Polynomial
Terms are defined as variables with co-efficient or constants related by addition or subtraction. Polynomials are classified as monomials, binomials and trinomials based on the number of terms. Two or more variables can also be multiplied together in a single term.
In the following example, the terms are:
Polynomial: \[3 + 10xy + 9x{y^2} + 16xyz\]
Terms: \[3,\,\,10xy,\,\,9x{y^2},\,\,16xyz\]
Factors of Terms of a Polynomial
Factors are constants or variables that can divide a term without leaving any remainder. For example, for the term \[5xy\], factors are \[5,\,x,\,y.\] Factorization of polynomials is done to solve polynomial equations.
Degree of a Polynomial
It is defined as the highest power of variables in the terms of a polynomial. The powers of all variables in a term should be added together to calculate the degree of the term. Then, the degrees of all terms of a polynomial should be compared to find the degree of the polynomial. If the degree of a polynomial is \[2\], it is called a quadratic polynomial. It has \[2\]roots. If the degree of a polynomial is \[3\], it is called a cubic polynomial, and it has \[3\] roots. For example, the degree of \[3{x^2} + 2\] is \[2\].
Addition and Subtraction of Polynomials
We can add or subtract like terms in two or more polynomials. Like terms are terms with the same variables in them. For example, if we add \[3x + 4\] and \[4x + 7\], we get \[(3x + 4) + (4x + 7)\,\, = \,\,(3x\, + \,4x)\, + \,(4\, + 7)\,\, = \,\,7x + 11\].
For the subtraction of \[3x + 4\] from \[4x + 7\],
\[(4x + 7)\,\, - \,\,(3x + 4)\,\, = \,\,(4x\, - \,3x)\,\, + \,\,(7\, - \,4)\, = \,x\, + \,3\]
Multiplication of a Polynomial with a Constant
To multiply a polynomial by a constant, we should multiply each term of the polynomial by the constant. For example, if we like to multiply \[3x + 5\] by 4, we should multiply each term by \[4\], \[4\,\,\times \,\,(3x\, + \,5) = \,12x\, + \,20\].
Interesting Facts
In algebra, polynomials are used to find unknown values in calculations.
Polynomials are used to study the relationship between two or more variables.
They can also be used to find the maximum and minimum value of a variable in a specified interval.
Solved Problems
Classify the following polynomials as monomial, binomial and trinomial.
\[\begin{array}{l}3x & & & 5x + 3\\45 & & & 3x + 4y\\7{x^3} & & & 2xy + 3{x^2} + {y^3}\\6{x^2} & & & 6{x^3} + 3x{y^2} + 4{y^4}\end{array}\]
Ans:
Monomials: \[3x,\,45,\,\,7{x^3},\,\,6{x^2}\]
Binomials: \[5x + 3,\,\,3x + 4y\]
Trinomials: \[2xy + 3{x^2} + {y^3},\,\,\,6{x^3} + 3x{y^2} + 4{y^4}\]
Find the degree of the polynomials below.
\[4{x^3} + 5x + 6{x^2}\]
Ans:
Since \[3\] is the highest among the degrees of all the terms, the degree of the polynomial is \[3\].
b) \[2x{y^2} + 15xy + 30x\]
Let us consider the term \[2x{y^2}\].
Here, the exponent of x = \[1\]
Exponent of y = \[2\]
The degree of the term, \[2x{y^2}\] = Exponent of x + Exponent of y
= \[1\, + \,2\]
= \[3\]
Similarly, we can find the degrees of other terms.
Since \[3\] is the highest among the degrees of all the terms, the degree of the polynomial is \[3\].
3. Add the polynomials \[4{x^2} + 3x + 4\] and \[5x + 3\].
Ans:
Adding the like terms,
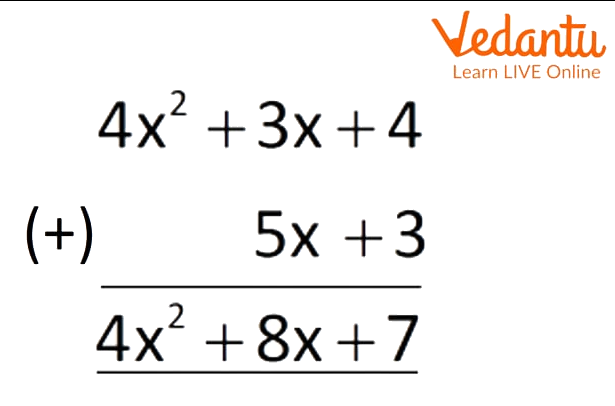
Addition of Polynomials
Practice Questions
Write the degree of the following polynomials.
\[4{x^3} + 2{x^2} + 5,\,\,2{x^2} + 3x,\,\,3xy,\,\,5x{y^2}\]
(Ans: 3, 2, 2, 3)
Add the polynomials \[3x + 2\] and \[5x + 4\].
(Ans: \[8x + 6\])
Conclusion
In this article, we learned about monomials, binomials, trinomials, and polynomials, with examples, and factors of polynomials. Polynomials are an important part of Mathematics that helps us deal with unknown quantities easily using mathematical expressions. We have also read about the applications of polynomials.
FAQs on Monomials, Binomials, Trinomials and Polynomials
1. What is called zero of a polynomial?
Let us consider a polynomial of one variable \[x\], \[f(x) = {x^2} - 4\]. The zeros of the polynomial are the roots of the equation \[f(x) = 0\]. In this case, \[{x^2} - 4 = 0\]. Therefore, \[x = 2,\,\,x = - 2\] are the roots of this polynomial.
2. What is called a linear polynomial?
A polynomial of degree one is called a linear polynomial. When we sketch the graph for this polynomial in a graph sheet, we will get a straight line.
3. Is \[\sqrt x \] a polynomial?
No. \[\sqrt x \] is not a polynomial because the exponent of \[x\] is \[1/2\] which is not an integer.
