




How to Identify Like and Unlike Terms in Algebra
The primary meaning of these two words is like and unlike. In other words, it means that they are both the same or they are different. For example, the letter “B” in the English language has a shape which is like “a” in the Arabic language. The same letter B has a form which is different from A or B on another hand. In mathematics, it also has a similar meaning as between two numbers but its meaning becomes stronger as it refers to objects which are not at all alike only difference consists of their numerical differences called arithmetic operations.
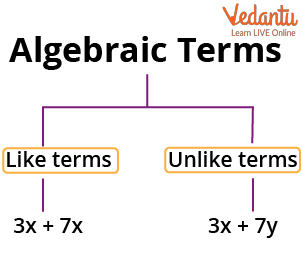
Like and Unlike Terms
Algebra is the study of mathematical concepts using a method of symbolic expression, wherein relations between quantities are expressed in terms of mathematical operations with symbols. Like and unlike terms can be found in various contexts, which forces students to consider their definitions and how they apply to the context or aim they are intended to serve.
What are Like Terms?
The like terms refer to terms in an algebraic expression with the same variable raised to the same power. Algebraic-like terms are terms that are similar to each other. These like terms in the algebraic expression can be combined to simplify the expression to derive the answer in a simple manner.
Like Terms Examples:
$14y-2y$: Here all the variables are $y$ to the power 1.
$14x^2+9x^2-x^2$: Here all the variables are $x$ to the power 2.
Rules of Addition of Like Terms
Consider another expression $5z + 12z + 32z$, here we see that the variables have the same exponent and the coefficients are also the same. We can further simplify this expression by adding the same variables from each other. This is possible since the variables and the exponents are the same. Hence, after simplifying the expression we get $(5 + 12 + 32)z = 49z$. The process of simplifying the expression is known as combining like terms.
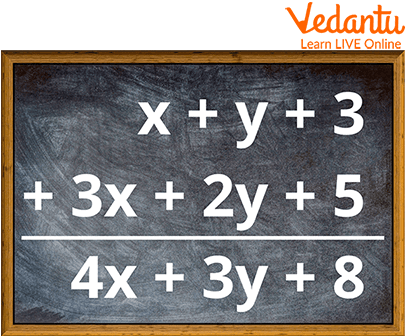
Addition of Like Terms
What are Unlike Terms?
Unlike terms refers to terms in an algebraic expression that does not have the same literal coefficients and cannot be raised to the same power.
Examples of unlike terms:
$3x+9y$
$13x+2xy-4y$
For example, the algebraic expression $3x + 9y$ where $x$ and $y$ are two different variables and different coefficients are known as unlike algebraic terms.
Rules of Addition for Unlike Terms
The simplification of expressions or combining like terms cannot be done on unlike terms, as the variables and exponents are not similar. For example, $8xy + 6y - 9x - 10x^2$, as seen here, there are different variables, exponents, and coefficients. This expression cannot be simplified as all the terms are different from each other.
Hence, for unlike terms there are no rules as they can’t be added.
How Can Like Terms and Unlike Terms be Separated?
When you focus on the words' variables, it is simple to distinguish between similar terms and those that are not. The variable component of like phrases will be the same, while the variable part of unlike terms will be different.
Similarities and Differences between Like and Unlike Terms
Like terms and unlike terms are expressions that contain different variables, but whose coefficients are all either positive or negative multiples of the same number.
In the case of like terms, the coefficients must be multiplied by the same number while in unlike terms examples they must be multiplied by different numbers. An example of like terms is: -3x + (-2x)
The only difference between these two terms is that the first term has a negative coefficient and the second term has a positive coefficient. One of the unlike terms examples is -4x + (-12x) + 8y
Steps to Find Like Terms
Isolate the variable.
Collect all like terms on one side of the equation or workbook page.
Connect like terms using any Maths operation (addition, subtraction, multiplication, or division) after the variable has been isolated.
Simplify and solve for x in terms of y.
Steps to Find Unlike Terms
Isolate the variable.
Collect all unlike terms on one side of the equation.
Find the coefficient of largest/smallest coefficient in each term found.
Simplify and solve for x in terms of y.

Some Examples of like Terms and Unlike Terms
These strategies are used to find these types of expressions and relate them to their intended context or target area: all problems can be done while solving a like and unlike terms worksheet.
Solved Examples
Q 1. What are the like and unlike terms in the given algebraic expression 5x2y + 4xy2 – xy – 9yx2 ?
Ans: Here, the terms are 5x2y, – 9yx2 since each of them has the same literal coefficient x2y.
And the unlike terms are 4xy2, – xy since each of them has different literal coefficients.
Q 2. Find out the like and unlike terms in the given algebraic expression 5x2 – 3y2 – 7x2 + 5xy + 4y2 + x2 – 2ab?
Ans: Here, the like terms are 5x2, – 7x2, x2 and – 3y2, 4y2.
And the unlike terms are 5xy and – 2ab
Q 3. In the algebraic expression, identify the like terms - 10xy + 3x3 + 21xy + 2x - xy - 6
Ans: Like terms: 10xy + 21xy - xy = 30xy
unlike terms: 7y - 5xy - 12x
Practice Questions:
Q 1. Group the like terms together:
(A)5x, -7y, -x, y/2, 5x/7, x and y
(B)2/3ab, -3ab, 5bc, -2/5bc, bc/4 and ab
(C)2/6ab
Ans: 5x, -x, 5x/7, x and -7y, y/2, y ( Option A )
Q 2. List out the like terms from each set:
(A)2m2n3, -3m2n3, 4mn2, 7m2n3
(B)12a2b, 3ab2, 4ba2, 2a2b
Ans: Like terms- 2m2n3, -3m2n3, 7m2n3
Unlike terms- 12a2b, 4ba2, 2a2b
Q 3. State whether the following statements are true or false:
(A) 8z has two terms 8 and z.
(B) Expression 10 + k has two terms 10 and k.
(C) xy and –yx are like terms.
Ans: False, True, True
Summary
A term in an algebraic expression may contain only a constant, just one variable, the product of two or more variables, or the product of the variable and the constant part. A single term can be created by combining one or more similar terms, but two dissimilar terms cannot be combined to create a single term. Like and unlike terms are discussed in brief with their examples. This article also contains some solved examples of the addition of like terms.
FAQs on Like Terms and Unlike Terms: A Simple Guide
1. Why do I need to learn about like and unlike terms?
In algebra, one of the most fundamental processes is the process of solving a system of equations. When we solve a system of equations, we are often presented with both like terms and unlike terms. If we do not understand how terms work or how to relate them to different situations, then it will be difficult for us to solve systems of equations. However, if one studies the information and the basic methods properly, nothing can be too difficult to solve.
2. How do we find like and unlike terms?
The easiest way to find these types of expressions is when they are written in the form of an equation. When they are written in the form of a problem or an activity, then we need to use human reasoning and analytical skills to solve these expressions. Using terms like algebra and unlike terms in algebra in different ways is one of the most important skills that students must have to succeed in algebra. For E.g. you can use the process of elimination if you have a system of equations with the only difference between them.
3. Can we add two or more, unlike algebraic terms?
No. The terms with the same variable with different exponents or different variables with the same exponents are called, unlike terms. Since an algebraic expression consists of two different variables, it cannot be combined or simplified further like "like algebraic terms”; only similar terms may be added or removed. One or more like terms are added together to form a single like term, but two unlike terms cannot be combined to form a single term.
4. What are the terms of addition?
An addition word is a mathematical expression that indicates the sum of two or more values. Addends are two or more values that are added together. An addition sentence consists of two or more addends, plus symbol(s), equal sign, and the sum.
5. What is the significance of algebraic expression?
Algebraic expressions are frequently used by people without them being aware of them, but they are still a part of mathematics in some way. Algebraic expressions are used in solving different and complex equations in Mathematics. Algebraic expressions are used for inference tasks in computer programming, for instance. In Economics, algebraic expressions are used to calculate revenue, costs, etc. Algebraic expressions are needed in many areas of Mathematics, including trigonometry, geometry, etc., to solve unknown angles and values. One can improve their aptitude and logical reasoning skills by studying algebra.























