Introduction to LCM
In mathematics, LCM stands for a least common number. It can be used to pair two objects against each other. In easy language, we can say that the smallest repeated multiple between two or more numbers is found using the Least Common Multiple (LCM) method. We can calculate LCM by using three methods.
Full Form of LCM
Each method has different formulas. LCM is also known as the lowest common number. In this chapter, we learn to solve LCM problems using all three methods and practice LCM sums. All three methods are explained below with examples.
LCM using Listing Method
LCM using Prime Factorization
LCM using Division Method.
Now understand these methods with the help of examples.
LCM by Listing Method
We can find out the common multiples of two or more numbers. Out of these repeated multiples, the LCM of two numbers can be calculated.
Let's take an example.
Q1. Find the LCM of numbers 4 and 5 by listing methods.
Ans: LCM of 4 and 5 by listing method:
4 is multiplied by: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ..
and 5 is multiplied by: 5, 10, 15, 20, 25, 30, 35, 40, …
The first common multiple of 4 and 5 is 20
according to the least method the LCM of 4 and 5 is 20.
LCM by Prime Factorisation Method
We can find out the prime factors of the numbers by using the prime factorization method. There are two steps to calculate the LCM using the prime factorization method.
Step 1: Put the numbers in the prime factored form
Step 2: The LCM of the given two numbers is the product of all the prime factors. (common factors will be included only once)
Understand this method using the example given below.
Q1. Find the least common multiple of 60 and 80
Ans: The prime factorization of 60 and 80 are:
60 = 2 × 2 × 3 × 5 = 2 × 2 × 3 × 5
80 = 2 × 2 × 2 × 5 × 2
LCM of 60 and 80 =2 × 2 × 3 × 2 × 5 × 2 = 240.
LCM by Division Method
To calculate the LCM of two numbers using the division method we have to follow the steps given below:
Step 1: Find a prime number that is a factor of at least one of the given numbers. Put this prime number to the left of the given numbers.
Step 2: If the prime number in step 1 is a factor of the number, divide the number by the prime and write the quotient below. If the prime number in step 1 is not a factor of the number, write the number in the row below as it is. Continue the steps until only one is left in the last row.
LCM Word Problems
1. Find the least common multiple (LCM) of 6 and 15 using the division method.
Ans:
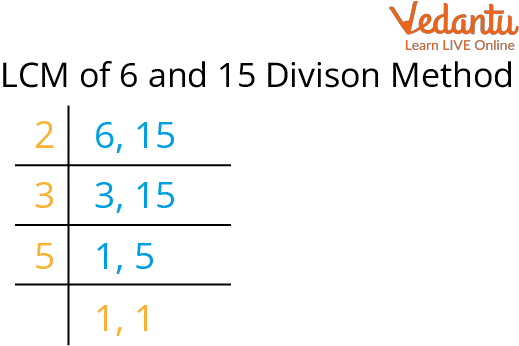
LCM by Division Method
LCM of 6 and 15 is 2 × 3 × 5 = 30.
2. What is the least common multiple of 980 and 9000 using the prime factorization method?
Ans: Prime factorization of 980 = 2 × 2 × 5 × 7 × 7 = 22 × 51 × 72 and
9000 = 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 = 23 × 32 × 53.
∴ LCM (980, 9000) = 23 × 32 × 53 × 72 = 441000.
Practice Questions
Q1. Find the LCM of 4, 6 and 12 by using the listing method.
Ans: 12
Q2. Find the LCM of 14 and 12.
Ans: 84
Summary
LCM is known as the lowest common number. LCM problems use three methods:
LCM using Listing Method
LCM using Prime Factorization
LCM using Division Method.
FAQs on Questions on Least Common Multiple (LCM)
1. What are the methods to find LCM?
LCM can be calculated by using three different methods. These are as follows:
A. LCM using the Listing Method: the LCM of two given numbers can be calculated with the common multiple of two given numbers.
B. LCM using Prime Factorization: The LCM of the given two numbers is the product of all the prime factors. In this method, we have to keep in mind that common factors will be included only once.
C. LCM using Division Method: The division method is the most common, fastest, and easiest of these three methods. It can be used for both small and large numbers.
2. What is LCM and what is the most common and easy way to find the LCM? Give an example.
The smallest repeated multiple between two or more numbers was found using the Least Common Multiple (LCM) method. There are three methods to find the LCM.
Three ways to find the LCM are listing method, prime factorization, and division. The division method is the most common, fastest, and easiest of these three methods. It can be used for both small and large numbers. For example
Example: Find the LCM of 36 and 48 by using the division method.
Divide the numbers (36, 48) by their prime factors to get the LCM of 36 and 48 by using the division method. First, we divide the number by a common prime number and use the prime factor to calculate LCM.
2 | 36 | 48 |
2 | 18 | 24 |
2 | 9 | 12 |
2 | 9 | 6 |
3 | 9 | 3 |
3 | 3 | 1 |
x | 1 | 1 |
Hence, LCM of 36 and 48 is 144.
