




How to Calculate LCM Using the Division Method Explained
Have you ever heard about LCM? The Least Common Multiple is the meaning of the abbreviation LCM. The lowest number that can be divided by both numbers is known as the least common multiple (LCM) of two numbers. It can also be computed using two or more numbers. Finding the LCM of a given set of numbers can be done in a variety of ways. Utilising the prime factorization of each number and then calculating the product of the highest powers of the shared prime factors is one of the quickest ways to determine the LCM of two numbers.

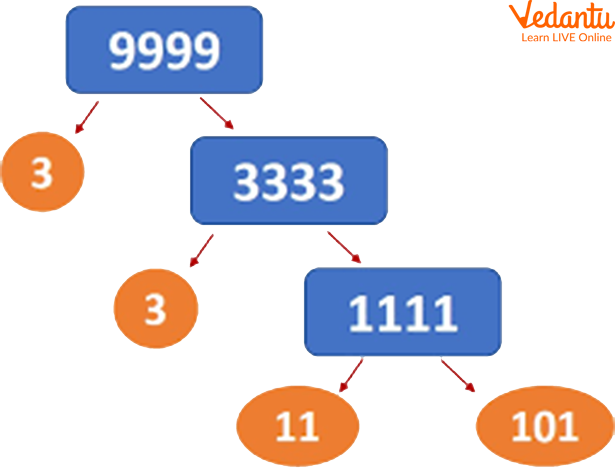
LCM by Common Division Method
LCM by Division Method
Diving Numbers
To find the LCM by division method, we write the given numbers in a row separated by commas, then divide the numbers by a standard prime number. We stop dividing after reaching the prime numbers. The product of common and uncommon prime factors is the LCM of given numbers.
Example: How to find LCM by the division method.
Ans: Here, we are given the numbers 20, 36, 63, and 67.
First, let us find their least common multiple using the division method.
First, we depict all numbers in a row, dividing them by a comma. Then we divide by a least prime number 2, which divides two of the numbers. Then we put the quotient directly under them, and the number which does not get divided remains the same. After dividing by 2, two numbers get separated, and the other remains the same. Then dividing by 3, two numbers get divided. Again, dividing by 3, two numbers get divided. Now dividing by 5, only one number gets divided. We are similarly divided by 7 and 67. So we get prime numbers by the division method as 2, 2, 3, 3, 5, 7, 67.
Difference Between Factors and Prime Factors
A number's factors are the numbers that are multiplied to get the original number. For example, 4 and 5 are factors of 20, i.e., 4 X 5 = 20, whereas prime factors of a number are prime numbers multiplied to obtain the original number. For example, the prime factors of 20 are 2, 2, and 5, i.e., 2 X 2 X 5 = 20.
Prime factorisation is similar to number factorisation but only considers prime numbers as factors (2, 3, 5, 7, 11, 13, 17, 19, and so on). As a result, the prime factors of a given number are those that ultimately divide the original number and cannot be divided into more factors.
All About Prime Factorisation

Prime Factorisation
A number can be expressed as a product of its prime factors using prime factorisation. The number 30 is not a prime number. The number 6 can be factored further into 2 X 3, where 2 and 3 are prime numbers. As a result, the prime factorisation of 30 is 2 X 3 X 5, with all factors being prime numbers.

Defining Factors
Steps for Finding Prime Factorisation Through Division
The standard division method is a very convenient way to find the LCM. In this prime factorisation method, we proceed as follows:
Put all of the numbers in a row, separated by commas.
Begin with the lowest prime number that exactly divides at least one of the given numbers.
In the following line, write down the quotients and any undivided numbers.
Repeat the procedure until 1 is the only common factor.
Determine the product of all divisors. Then, it is the necessary LCM.
To understand better, check the below example.
Example: Determine the LCM of the numbers 36, 48, and 72.
Ans: The calculation is given in the picture as follows:

LCM of the Numbers 36, 48, and 72
LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144
Summary
The smallest number that is a multiple of all the numbers in a set is called the Least Common Multiple (LCM) of the group of numbers. For instance, 80 is the smallest number that is both a multiple of 16 and a multiple of 20, making it the LCM of 16 and 20. The LCM of two or more numbers can be calculated in some ways. LCM is defined to be 0 if either of the two is 0. The sum of all relative prime numbers is known as the LCM.
FAQs on LCM by Division Method: Easy Steps & Key Examples
1. What does prime factorization mean?
Prime factorisation is writing a number as the product of prime numbers. Prime numbers are those with only two factors. Any number can be prime factorised, meaning it can be represented as a product of prime numbers. A number can be expressed as a product of its prime factors using prime factorization. Take the number 30 as an example. Although we know that 30 = 5, 6, 6 is not a prime number. The number 6 can be factored further as 2, 3 where 2 and 3 are prime numbers. As a result, the prime factorization of 30 is 2, 3, and 5 with all factors being prime numbers.
2. What does LCM stand for?
The LCM of any two numbers is the value that is evenly divisible by the two given numbers. Least Common Multiple is an abbreviation for Least Common Multiples. It's also known as the Least Common Divisor (LCD). LCM (4, 5) = 20, for example. In this case, the LCM 20 is divisible by both 4 and 5, so the divisors of 20 are 4 and 5. When performing any arithmetic operation with fractions, such as addition or subtraction, LCM is used to make the denominators common. This procedure facilitates the simplification process.
3. What are the factors of the number?
A number's factors are numbers that divide the original number evenly or exactly. A factor is defined as a whole number that can divide a larger number evenly. A fraction is not a factor. Each prime number has only two factors: 1 and the number itself, whereas all composite numbers have more than two factors, including prime factors. An algebraic expression's factors are the values that can divide the given expression.
Here are some examples:
Factors of 2 = 1 and 2
Factors of 10 = 1, 2, 5 and 10











