Round to the Nearest Tenth

A decimal is a number divided into two parts: a whole and a fraction. Between integers, decimal numbers express the numerical value of complete and partially whole amounts. Rounding is the act of reducing a number while maintaining its value.

Although the outcome is less accurate, it is easier to use. To estimate values without writing a tonne of digits to the right of the decimal point, round decimals. You can round decimals to the closest whole number, nearest tenth, nearest hundredth, or nearest thousandth decimal place.

Nearest Tenth of a Decimal:

We must round a number to the nearest tenth to obtain the hundredth place, placed to the right of the tenth place. If the digit in the hundredth place is five or greater, the digit in the tenth place must be raised by one.

If it is 4 or less, the tenth-place digit stays the same. All the numerals to the right of the tenth spot should be changed to 0. In other words, we will stop at the tenth place rather than rounding a number to the nearest tenth.

Rounding Decimals to the Nearest Tenth:

To write a decimal number up to one decimal place, round it to the nearest tenth. This is done by leaving one digit after the decimal point after rounding. To round to the closest tenth, we must locate the digit in the 'tenths' location and pay attention to the digit to its right in the given number. The first digit following the decimal point is considered to be in the tenth place.

Round to the Nearest Tenth:

Do you know how to Round to the Nearest Tenth? Today, we will see the rules necessary to follow to round to the nearest tenth value given below:

At first, we will see how to round off when the hundredth number is more than 5. For example, take the number 4.569.

• Watch the number that has to be rounded, i.e., the tenth place number or the first digit following the decimal point.

• Observe the digit in the "hundredths" place, which is to the right of the digit in the tenth place, after marking the digit in the "tenths" place.

• If the digit in the hundredth place is 5 or higher, we increase the tenth place by 1, add 1 to the digit in the hundredth place, and then put 0 in all the digits to the right.

Round to the nearest tenth

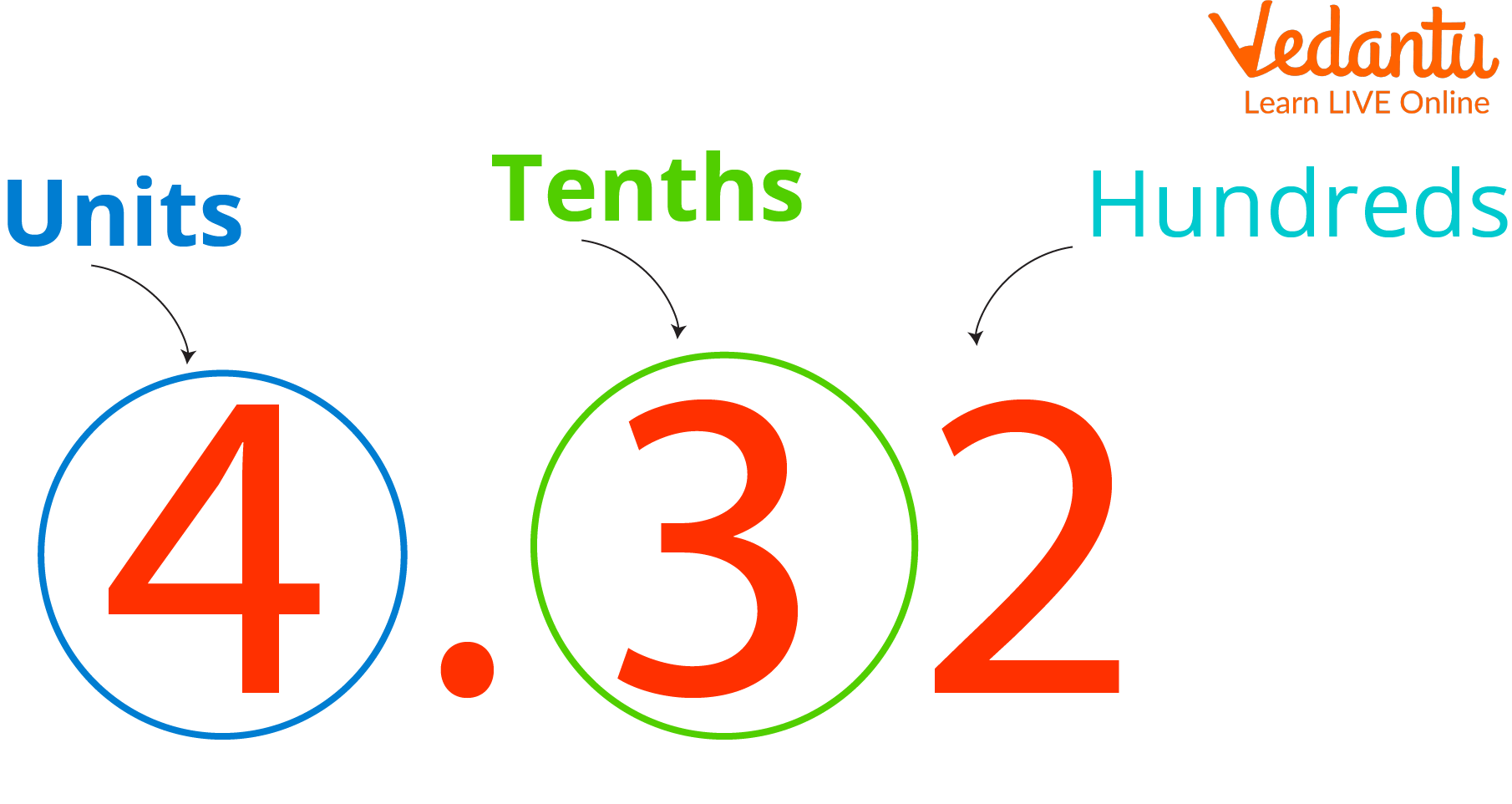
Now, we will see how to round off when the hundredth number is less than 5. For example, take the number 4.32.

• Watch the number that has to be rounded, i.e., the tenth place number or the first digit following the decimal point.

• Observe the digit in the "hundredths" place, which is to the right of the digit in the tenth place, after marking the digit in the "tenths" place.

• The tenth place digit will remain unchanged as the digit in the hundredth place is less than 5, and we write 0 in the hundredth place and all the places to its right.

Example for Rounding to the Nearest Tenth:

Let us look at some rounds to the nearest tenth examples:

Example 1: Round 263.57 to the nearest tenth.

Solution: The tenth digit, in this example, 5, is the first integer to the right of the decimal point. The digit after the decimal point, 7, is more than 5. In this instance, we must add 1 to the number 5.

Hence, the number will be 263.6.

Example 2: Round 6.62 to the nearest tenth.

Solution: The tenth digit in this example is 6. The digit after the tenth place is 2, less than 5, so the digit remains unchanged.

Hence, the number will be 6.6.

Conclusion:

Therefore, rounding off to the nearest tenth is learned in this article. We use this idea daily to calculate our grocery costs and other bills; thus, it is quite significant. Any integer can now be rounded to the closest tenth by following the methods given.