




Step-by-Step Guide: Finding HCF and LCM of Polynomials
Do you find working with LCM and HCF exciting? The Least Common Multiple is abbreviated as LCM. It is defined as the smallest number that, when multiplied by both of the given numbers, gives a product that is less than or equal to the original number. The Highest Common Factor is abbreviated as HCF. It is the largest positive number that divides the given numbers. The LCM and HCF of 3, 4, and 5 are 60 and 1, respectively. In this article, you will learn how to find the HCF and LCM of algebraic expressions, the relation between HCF and LCM of two polynomials, and HCF and LCM tricks, along with some solved examples of HCF and LCM.
Finding the HCF and LCM of Algebraic Expressions
The most convenient method to find the HCF and LCM of algebraic expressions is prime factorisation. Steps to be followed while finding the HCF and LCM of algebraic expression are given below:
Write the given algebraic expressions
Separate terms corresponding to each algebraic expression
Find the prime factors of all the terms
To obtain the HCF of algebraic expression, take the common of all the prime factors of two polynomials.
To obtain the LCM of algebraic expression, take the product of all its prime factors.
For example, the HCF and LCM of algebraic expressions $2 \mathrm{y}$ and $14 x \mathrm{y}^3$ are given by writing their prime factors, i.e. 2, $y$ and $(7)(2), x,(y)(y)(y)$ respectively.
HCF of the algebraic expressions is $2 \mathrm{y}$
LCM of the algebraic expression is $14 x y^3$.
What is the Relation Between LCM and HCF of Two Polynomials?
The relation between LCM and HCF of two polynomials is given below:
The product of two polynomials is equal to the product of their LCM and $\mathrm{HCF}$, i.e. $\mathrm{p}(\mathrm{x}) \times$ $q(x)=\{$ L.C.M of $p(x)$ and $q(x)\} \times \{$ H.C.F of $p(x)$ and $q(x)\}$, where $p(x)$ and $q(x)$ are two polynomials.
For example: Let the two polynomials be $p(x)=3 x y$ and $q(x)=2 x^2$ LCM of $p(x)$ and $q(x)$ is $6 x^2 y$
HCF of $p(x)$ and $q(x)$ is $x$
The product of two polynomials, $p(x)$ and $q(x)$ is $3 x y \times 2 x^2=6 x^3 y \quad$ ____(1)
Product of their HCF and LCM is given by $x \times 6 x^2 y=6 x^3 y \quad$ ____(2)
Equations 1 and 2 show that the product of two polynomials is equal to their HCF and LCM products.
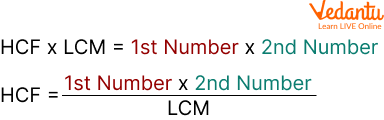
HCF and LCM of Two Polynomials
In the above image, the number represents the polynomials.
HCF and LCM Tricks
Here are some HCF and LCM tricks that can help students to find the HCF and LCM of algebraic expressions easily:
If the expression is a perfect square, the HCF and LCM are the value of the highest number in the expression.
If the expression is not a perfect square, the HCF is the value of the highest number plus the value of the lowest number.
If the expression is not a perfect square, the LCM is the value of the highest number minus the value of the lowest number.
Solved Examples of HCF and LCM
Q 1. Find the LCM and HCF of 9a3b2 and 15b3c2
Ans: Find the LCM and HCF of $9 a^3 b^2$ and $15 b^3 c^2$. Here,
Prime factors of 1st expression, $9 a^3 b^2$ are $3 \times 3 \times a \times a \times a \times b \times b$
Prime factors of 2nd expression, $15 b^3 c^2$ are $3 \times 5 \times b \times b \times b \times c \times c$
HCF $=3 \times \mathrm{b} \times \mathrm{b}=3 \mathrm{~b}^2$
LCM $=3 \times 3 \times 5 \times a \times a \times a \times b \times b \times b \times c \times c=45 a^3 b^3 c^2$
Thus the LCM and HCF of $9 a^3 b^2$ and $15 b^3 c^2$ are $45 a^3 b^3 c^2$ and $3 b^2$, respectively.
Q 2. Find the HCF of 6xy2z, 8x2y3z2, 12x3y3z3.
Ans: The prime factors are as following:
$\Rightarrow 6 x y^2 z=2 \times 3 \times x \times y \times y \times z$
$\Rightarrow 8 x^2 y^3 z^2=2 \times 2 \times 2 \times x \times x \times y \times y \times y \times z \times z$
$\Rightarrow 12 x^3 y^3 z^3=2 \times 2 \times 3 \times x \times x \times x \times y \times y \times y \times z \times z \times z$
HCF of $6 x y^2 z, 8 x^2 y^3 z^2 \text { and } 12 x^3 y^3 z^3=2 \times x \times y \times y \times z=2 x y^2 z$
Practice Questions
Q 1. Find the LCM and HCF of 21xy2 and 63x2y.
Ans: HCF: 21xy
LCM: $63 x^2 y^2$
Q 2. Find the HCF of 11ab and 55a.
Ans: $11 a$
Q 3. What is the LCM of 27pqr and 3p2q2 ?
Ans: $27 p^2 q^2 r$
Summary
This article has covered the most important topic used in every mathematical calculation. Here we have learned how to find the HCF and LCM of algebraic expressions, what is the relation between LCM and HCF, and the HCF and LCM tricks. The relation between HCF and LCM of two polynomials states that the product of two polynomials is equal to that of their LCM and HCF. We also discussed some solved examples of HCF and LCM, along with some practice questions that the students need to solve by themselves for a better understanding of the concept.
FAQs on HCF and LCM of Two Polynomials Explained
1. What do HCF and LCM mean in the context of two polynomials?
In polynomials, the Highest Common Factor (HCF) is the polynomial of the highest possible degree that is a factor of both given polynomials. It is also known as the Greatest Common Divisor (GCD). The Least Common Multiple (LCM) is the polynomial of the lowest possible degree that is a common multiple of both given polynomials.
2. What is the step-by-step method to find the HCF of two polynomials?
To find the HCF of two polynomials, follow these steps as per the CBSE syllabus for the 2025-26 session:
Step 1: Factorise each polynomial completely into its irreducible factors (factors that cannot be broken down further).
Step 2: Identify all the factors that are common to both polynomials.
Step 3: The HCF is the product of these common factors, with each factor raised to the lowest power it appears in any of the factorisations.
3. How do you calculate the LCM of two polynomials?
To find the LCM of two polynomials, the standard method involves these steps:
Step 1: First, resolve each polynomial into its irreducible factors.
Step 2: List all the distinct factors that appear in any of the polynomials.
Step 3: The LCM is the product of these distinct factors, with each factor raised to the highest power it appears in any of the factorisations.
4. What is the fundamental relationship between two polynomials and their HCF and LCM?
There is a crucial relationship that connects two polynomials with their HCF and LCM. For any two polynomials, let's say p(x) and q(x), the product of the polynomials is equal to the product of their HCF and LCM. The formula is: p(x) × q(x) = HCF(p(x), q(x)) × LCM(p(x), q(x)). This formula is extremely useful for finding the LCM if the HCF is known, or vice versa.
5. Why is finding the LCM of polynomials important when simplifying algebraic fractions?
Finding the LCM is a fundamental application when you need to add or subtract algebraic fractions. The denominators of these fractions are polynomials. To combine them, you need a common denominator, and the Least Common Denominator (LCD) is precisely the LCM of the polynomial denominators. Using the LCM ensures that the resulting fraction is in its simplest form and avoids dealing with unnecessarily complex expressions.
6. Can the HCF of two non-zero polynomials be just a number (a constant)?
Yes, the HCF of two polynomials can be a constant. This happens when the polynomials do not share any common polynomial factors. For example, if we have p(x) = 2(x + 1) and q(x) = 3(x - 1), they have no common variable factors. The HCF of the numerical coefficients 2 and 3 is 1. Therefore, the HCF of p(x) and q(x) is 1, which is a constant.
7. How does the concept of HCF apply to real-world problems?
While HCF of numbers has direct applications in splitting items into equal groups, the HCF of polynomials is a more abstract concept primarily used in higher mathematics and engineering. It is crucial for simplifying complex rational expressions in fields like control systems, signal processing, and physics, where polynomial fractions are used to model system behaviour. Simplifying these models makes them easier to analyse and understand.
8. What is a common mistake to avoid when finding the HCF or LCM of polynomials?
A common mistake is incorrectly handling the signs or numerical coefficients. When factoring a polynomial like -x² + 9, students might forget to factor out the negative sign first. The correct factorization is -(x² - 9), which becomes -1(x - 3)(x + 3). This '-1' is a factor and must be considered when identifying common factors for both HCF and LCM calculations, especially if another polynomial also has a negative leading coefficient.

















