How to Recognize and Apply Geometric Solids in Everyday Math
We call geometry a branch of Math that focuses on the measurement and relationship of lines, angles, surfaces, solids, and points. An example of geometry is the calculation of a triangle's angles. Shapes that we study in geometry are 2-d and 3-d.
2-d shapes have two dimensions, such as x and the y-axis. Also, it has length and width. Examples are circle, square, rectangle, and so on. However, shapes like sphere, hemisphere, cylinder, cube, and cuboid have three dimensions, i.e., x, y, and z-axis. The walls of your room have a 3-d structure. Also, these shapes have length, height or depth, and width.
The walls of your room have a kind of 3-d space which you live in. And the geometry of this 3-d space is called the solid geometry or simply we can say it is a geometric solid.
What is Geometric Solid?
Before starting with what solid geometry is, let us go through some of the common 3-d shapes:

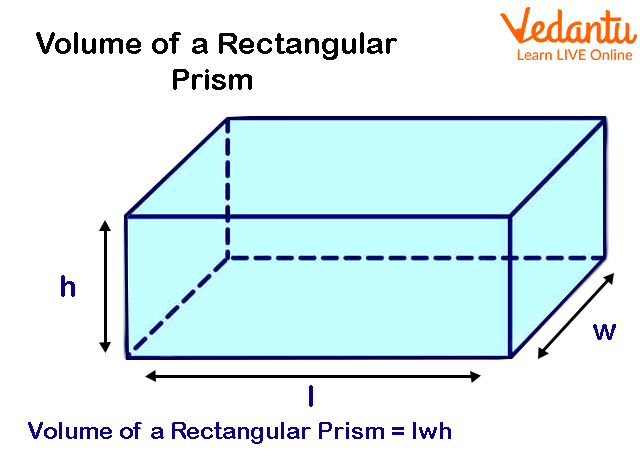
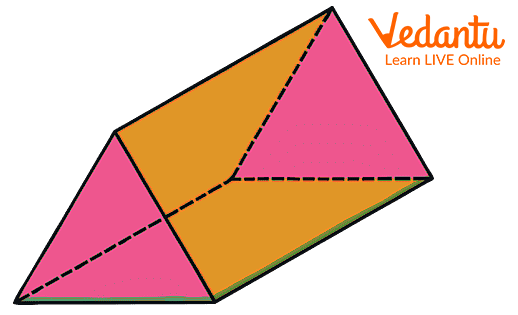
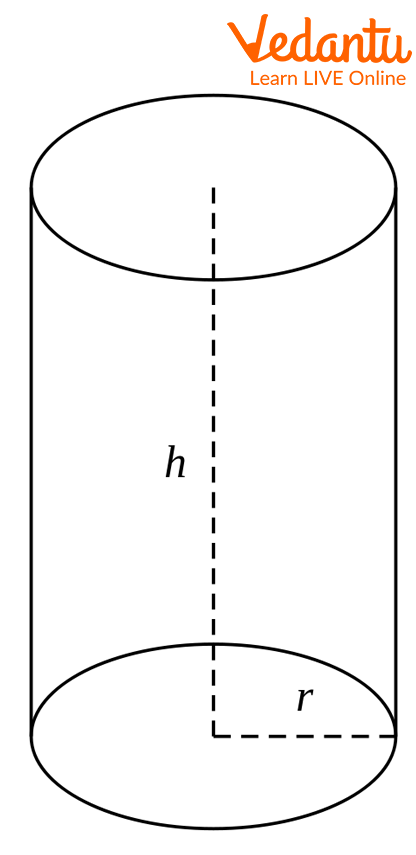
Image: Solid common 3-d shapes
We understood from the above text that these shapes have three dimensions having length, depth, and width. These shapes carry the following properties:
Capacity or volume (think of how much water it could hold).
Surface area (think of the amount of area covered by the surface of something).
How many vertices (corner points), faces, and edges do they have.
Formulas of Solid Geometry
The following table gives the volume formulas and surface area formulas for the following 3-D solid shapes:
Solved Examples of Geometric Solid
1. Find the volume and surface area of a cube whose side is 7 cm.
Solution:
Side, a = 7 cm.
The volume of a cube = a3 cubic units
V = 73
V = 7 x 7 x 7
V = 343 cm3
Therefore, the volume of a cube is 343 cubic centimeter.
The surface area of a cube = 6a2 square units
SA = 6 x (7)2 cm2
SA = 6 x (49)
SA = 294 cm2
Therefore, the surface area of a cube is 294 square centimeters.
2. Find the total surface area of a cuboid of dimensions 9 cm × 8 cm × 6 cm.
Solution:
Given dimensions of a cuboid: 9 cm x 8 cm x 6 cm
That means length = l = 9 cm, breadth = b = 8 cm, and height = h = 6 cm.
Total surface area of a cuboid = 2 (lb + bh +hl)
= 2 (9 x 8 + 8 x 6 + 6 x 9)
= 2 (72 + 48 + 54 )
= 348 cm2
Hence, the total surface area of the cuboid is 348 cm2.
From the above text on geometric solid, we understand that solid geometry is regarded with 3-D shapes. Examples of three-dimensional solid shapes are cubes, rectangular solids, prisms, cylinders, spheres, cones, and pyramids.
FAQs on Geometric Solids: Definition, Key Formulas & Solved Questions
1. What are geometric solids in mathematics?
Geometric solids, also known as three-dimensional (3D) shapes, are objects that occupy space. Unlike 2D shapes, they have three dimensions: length, width, and height. The key characteristics of these solids are their faces (the flat or curved surfaces), edges (where two faces meet), and vertices (the corners where edges meet).
2. What are the two main classifications of geometric solids?
Geometric solids are broadly classified into two main types based on their surfaces:
Polyhedrons: These are solids made entirely of flat surfaces (polygons). Each face is a polygon, and examples include cubes, pyramids, and prisms.
Non-Polyhedrons: These are solids that have at least one curved surface. Common examples include spheres, cylinders, and cones.
3. Can you provide some examples of geometric solids and their real-world counterparts?
Certainly. Many everyday objects are examples of geometric solids:
Cube: A standard die, a sugar cube.
Cuboid: A book, a shoebox, a brick.
Sphere: A football, a globe, a marble.
Cylinder: A soda can, a pipe, a battery.
Cone: An ice cream cone, a party hat, a funnel.
4. What are the key properties of common geometric solids like a cube, cylinder, and sphere?
The properties of these solids differ significantly:
Cube: It has 6 square faces, 12 equal edges, and 8 vertices.
Cylinder: It has 2 flat circular faces, 1 curved surface, 2 circular edges, and 0 vertices.
Sphere: It has only 1 continuous curved surface, with 0 faces, 0 edges, and 0 vertices.
5. What is the fundamental difference between a prism and a pyramid?
The main difference lies in their structure and side faces. A prism has two identical and parallel bases, and its side faces are parallelograms (often rectangles). A pyramid, on the other hand, has only one base, and its side faces are triangles that meet at a single point called the apex or vertex.
6. How are the key formulas for the volume of a cuboid and a cylinder different?
The formulas reflect their different shapes. The volume of a cuboid is calculated by multiplying its three dimensions: Volume = length × width × height. For a cylinder, the volume is found by multiplying the area of its circular base by its height: Volume = π × radius² × height. The cuboid's formula is based on linear dimensions, while the cylinder's incorporates the area of its circular base.
7. Why is a sphere considered a geometric solid if it has no flat faces, edges, or vertices?
A shape is defined as a geometric solid if it is a three-dimensional figure that encloses a volume. While polyhedrons like cubes are defined by their flat faces, edges, and vertices, a sphere fits the primary definition of a solid by occupying space. It is a non-polyhedron, defined as the set of all points in 3D space that are equidistant from a central point. Its defining property is its volume and surface area, not its faces or edges.
8. How does Euler's formula apply to geometric solids?
Euler's formula is a fundamental principle that applies specifically to polyhedrons (solids with flat faces). It provides a relationship between the number of faces (F), vertices (V), and edges (E) of any simple polyhedron. The formula is F + V - E = 2. For example, for a cube, we have 6 faces, 8 vertices, and 12 edges. Plugging this into the formula: 6 + 8 - 12 = 2. This formula is a powerful tool to verify the structure of polyhedrons.