How to Multiply Fractions with Formula and Examples
In this article, we learn to find the product of fractions. Fractions are defined by a numerical value that represents a part of a whole. A fraction can be a portion or section of any quantity out of a whole, whereas the whole can be any number, a specific value, or a thing. When a fraction is multiplied by another fraction the resultant is also a fraction or a whole number and it's called the product of fractions. We are aware that a fraction has two main parts: a numerator and a denominator. In order to multiply any two fractions, we should multiply the numerators and denominators, respectively. Before finding the product of fractions, let’s discuss the types of fractions.
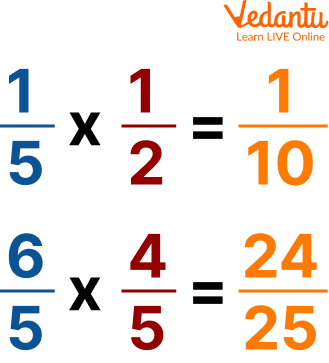
Product of fractions
Fractions and Their Types
The fractions define the ratio of two numbers. If a fraction is represented as $\dfrac{a}{b}$, where ‘a’ is the numerator and ‘b’ is the denominator. The three main types of fractions are mixed, proper, and improper fractions.
When a fraction's numerator is less than its denominator.
Example: $\dfrac{1}{2}$, $\dfrac{3}{4}$
Improper fractions
When a fraction's numerator is greater than its denominator.
Example: $\dfrac{3}{2}$, $\dfrac{5}{3}$
Mixed Fraction
A result that includes both a whole number and a fraction.
Examples: $3 \dfrac{1}{4}$, $4 \dfrac{1}{5}$
The Product of the Fractions
The product of the fractions is defined as the product of two or more fractions in the form of a fraction or the variables.
How to Find the Product of the Fractions?
The steps to find the product of the fractions:
Step1: Multiply the numerator with the numerator.
Step2: Multiply the denominator with the denominator.
Step3: Simplify the fractions.
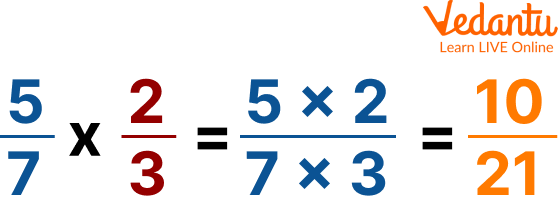
Steps of finding the product of fractions
If “$\dfrac{a}{b}$” and “$\dfrac{c}{d}$” are the two fractions, then the formula for product of fractions is:
$\dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{ac}{bd}$
Product of the Fraction = $\dfrac{\text{Product of the Numerators}}{\text{Product of the Denominators}}$
Example:
Q. Find the product of fractions $\dfrac{3}{2}$ and $\dfrac{4}{5}$.
Ans. The product of the given fractions is:
$\dfrac{3}{2} \times \dfrac{4}{5}$ = $\dfrac{12}{10}$
On simplification, we get $\dfrac{6}{5}$.
Therefore, the product of $\dfrac{3}{2}$ and $\dfrac{4}{5}$ is $\dfrac{6}{5}$.
How to Find the Product of Mixed Fractions?
When a fraction contains both a whole number and a proper fraction, it is called a mixed fraction. Steps are following:
Step 1: Make improper fractions from the mixed fractions.
Step 2: Multiply the Fractions.
Step 3: Convert the product back to Mixed Fractions.
Find the Product of Fractions with Whole Numbers
To find the product of fractions with whole numbers, we apply the rule of multiplying the numerators, then the denominators, and then reducing them to the simplest terms. Whole numbers are written in the fractional form by adding ‘1’ to the denominator. A fraction can be used to represent a whole number, like, $3=\dfrac{3}{1}$, in which 3 is the numerator and 1 as the denominator.
You can find the product of any fraction by a whole number simply by multiplying the numerator by the whole number.
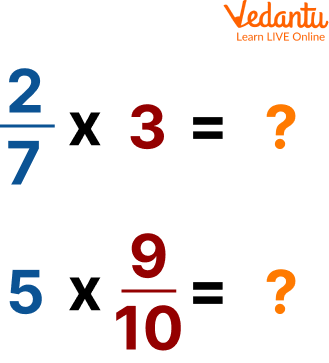
Examples of the product of fractions with whole numbers
Example1: Find the product of $\dfrac{4}{5} \times 6$.
Solution: Steps to find the product of fractions:
Step1: 6 is a whole number, it may be expressed as $\dfrac{6}{1}$.
Step2: This means, $\dfrac{4}{5} \times \dfrac{6}{1}$.
Step3: Multiply the numerators, $4 \times 6 = 24$.
Step4: Multiply the denominators, $5 \times 1 = 5$.
Step5: The result is $\dfrac{24}{5}$ which cannot be further reduced.
Example2: Find the product of the fraction $4 \times \dfrac{5}{12}$ or find the fraction.
Solution: Multiply the numerators, $4 \times 5 = 20$.
The denominator stays the same.
$4 \times \dfrac{5}{12} = \dfrac{20}{12}$.
To simplify this fraction, both 20 and 12 are divisible by 4.
$4 \times \dfrac{5}{12} = \dfrac{20}{12} = \dfrac{5}{3}$
It cannot be divided further.
Find the Product of the Mixed Fractions
To find the product of the mixed fractions, before multiplication, we must convert the mixed fractions into improper fractions. For example, if the fraction is $3 \dfrac{2}{3}$, we should change it to $\dfrac{11}{3}$.
Example: Find the product of $2 \dfrac{2}{3}$ and $2 \dfrac{3}{4}$.
Ans: The following steps used to find the product of the mixed fractions.
Step1: Convert the mixed fractions to improper fractions, i.e., $2 \dfrac{2}{3} = \dfrac{8}{3}$ and $2 \dfrac{3}{4} = \dfrac{11}{4}$.
We get $\dfrac{8}{3} \times \dfrac{11}{4}$
Step2: Now multiply the numerators, and then multiply the denominators. We get $\dfrac{88}{12}$.
Step3: Now, reduce the resulting fraction by the lowest possible number of terms, then we get $\dfrac{22}{3}$.
Step4: Finally, change the result back to a mixed fraction, i.e., $7 \dfrac{1}{3}$.
Find the Product of the Fractions Calculator
A free online calculator tool is used to get the product of the fractions called the multiply fractions calculator. The steps that followed to use the calculator for multiplying fractions:
Step1: Type the fractions into the appropriate input field.
Step2: Now to obtain the product, click the "Multiply" button.
Step3: Finally, the output field will show the result of two fractions.
Practice Questions
Q 1. Find the product of the following fractions:
$\dfrac{7}{11}$ by $\dfrac{3}{10}$ (Ans: $\dfrac{21}{110}$ )
$\dfrac{3}{5}$ by 11 (Ans: $\dfrac{33}{5}$)
$4 \dfrac{2}{3}$ by 5 (Ans: $23 \dfrac{1}{3}$)
$3 \dfrac{1}{2}$ by $7 \dfrac{2}{3}$ (Ans: $26 \dfrac{5}{6}$)
Q 2. In a basket, there are 60 balls, and $\dfrac{2}{3}$ of them are red balls. Find the number of red balls there.
Ans: 40 red balls
Summary
In this article, we got to know about finding the product of fractions. Here we specifically learned to find the product of fractions with whole numbers and the product of mixed fractions with different methods. To find the product of fractions, first, simply reduce the fraction to its lowest term. The product of fractions is always obtained in $\dfrac{a}{b}$ form.
FAQs on Finding the Product of Fractions Made Easy
1. How do you find the product of fractions?
To find the product of fractions, multiply the numerators together and multiply the denominators together. Follow these steps:
- Step 1: Multiply the numerators (top numbers).
- Step 2: Multiply the denominators (bottom numbers).
- Step 3: Simplify the fraction if possible.
2. What is the formula for multiplying fractions?
The formula for multiplying fractions is (a/b) × (c/d) = (a × c)/(b × d). Here:
- a and c are numerators.
- b and d are denominators (b, d ≠ 0).
3. Do you need a common denominator to multiply fractions?
No, you do not need a common denominator when multiplying fractions. Unlike addition or subtraction, fraction multiplication only requires multiplying across:
- Numerator × Numerator
- Denominator × Denominator
4. How do you multiply mixed numbers?
To multiply mixed numbers, first convert them to improper fractions, then multiply. Steps:
- Step 1: Convert to improper fractions.
- Step 2: Multiply numerators and denominators.
- Step 3: Simplify the result.
5. How do you simplify fractions before multiplying?
You can simplify before multiplying by using cross-cancellation. Steps:
- Step 1: Look for common factors between a numerator and a denominator diagonally.
- Step 2: Divide both by their greatest common factor (GCF).
- Step 3: Multiply the simplified numbers.
6. What happens when you multiply a fraction by a whole number?
When multiplying a fraction by a whole number, write the whole number as a fraction over 1 and multiply normally. Formula: (a/b) × n = (a × n)/b. Example: 3/5 × 4 = (3 × 4)/5 = 12/5 or 2 2/5.
7. Why does multiplying fractions sometimes give a smaller number?
Multiplying fractions gives a smaller number when both fractions are less than 1 because you are taking a part of a part. For example, 1/2 × 1/3 = 1/6, which is smaller than both 1/2 and 1/3. This happens because fraction multiplication represents scaling down.
8. Can you give an example of multiplying proper fractions?
An example of multiplying proper fractions is 3/4 × 2/5 = 6/20 = 3/10. Steps:
- Multiply numerators: 3 × 2 = 6.
- Multiply denominators: 4 × 5 = 20.
- Simplify by dividing by 2.
9. What are common mistakes when finding the product of fractions?
Common mistakes when finding the product of fractions include:
- Adding instead of multiplying numerators and denominators.
- Forgetting to simplify the final answer.
- Not converting mixed numbers to improper fractions.
- Incorrect cross-cancellation.
10. How do you check your answer after multiplying fractions?
You can check your answer by simplifying fully and estimating the size of the result. Steps:
- Ensure the fraction is in simplest form.
- Estimate: if both fractions are less than 1, the product should be smaller.
- Recalculate using the formula (a/b) × (c/d) = (a × c)/(b × d).
