Factors of 78 Explained with Easy Steps

As we all know that $78$ is an even composite number, it has some proper factors i.e., the factors other than $1$ and $78$ itself. $78$ has a total of $8$ factors: $1, 2, 3, 6, 13, 26, 39, 78$. Naturally, a prime factor of $78$ is a factor of $78$ which is also a prime number; hence, from the above list of factors, we can see that $2$, $3$, and $13$ are the only prime factors of $78$. 

$78$ is not a perfect square; prime factors of $78$ are $2$, $3$, and $13$ and each of them occurs only one time in the prime factorization of $78$ i.e., $78=2\times 3\times 13$. Also, the pair factors of $78$ are: $(1,78)$, $(2,39)$, $(3,26)$ and $(6,13)$.

What Are the Factors of 78?

Factors of $78$ are the integers that completely divide it without leaving any remainder. Let us first find out the integers that fully divide $78$:

$78\div 1=78$ $78\div 78=1$

$78\div 2=39$ $78\div 39=2$

$78\div 3=26$ $78\div 26=3$

$78\div 6=13$ $78\div 13=6$

Hence, by definition of factor of a number, $78$ has a total of $8$ factors: $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$.

If we consider negative factors also, then $78$ has a total of $16$ factors, viz., $\pm 1,\text{ }\pm 2,\text{ }\pm 3,\text{ }\pm 6,\text{ }\pm 13,\text{ }\pm 26,\text{ }\pm 39,\text{ }\pm 78$.

Method of Finding the Factors of 78: Division Method

In this section, we will learn how to find the factors of $78$. There are several methods of finding the factors of an integer. Here, we will follow the Division Method. In this method, we will divide $78$ successively by the integers starting from $1$, $2$, $3$, and so on and whenever we get the remainder $0$, then the corresponding divisor and quotient will be treated as the factors of $78$.

This process continues till any one of the numbers is repeated. This process can be summarised as follows:

1. As $1$ divides any number, $1$ is a factor of $78$ and since $78\div 1=78$, the quotient $78$ is also a factor of $78$.

2. Since $78$ is an even number, it is divisible by $2$. Also, $78\div 2=39$. So, the quotient $39$ also divides $78$ completely. Thus, $2$ and $39$ are factors of $78$.

3. The sum of the digits in $78$ is $7+8=15$ which is divisible by $3$. So, $3$ divides $78$ without leaving any nonzero remainder, and also, $78\div 3=26$. Thus, $3$ and $26$ are factors of $78$.

4. As $78=4\times 19+2$, $4$ does not divide $78$ as it leaves a nonzero remainder $2$ while dividing $78$.

5. Since the last digit of $78$ is $8$ which is not $0$ and $5$, so, $5$ does not divide $78$ and hence, is not a factor of $78$.

6. As $78$ is divisible by both $2$ and $3$, it is divisible by $6$. Also, $78\div 6=13$. So, $6$ and $13$ are factors of $78$.

7. Since $78=7\times 11+1$, $7$ cannot divide $78$ fully as it leaves a non zero remainder of $1$. Thus, $7$ and $11$ are not factors of $78$.

8. Since $78=8\times 9+6$, $8$ cannot divide $78$ completely as it leaves a nonzero remainder of $6$. Thus, $8$ and $9$ are not factors of $78$.

9. Since $78=9\times 8+6$, $9$ cannot divide $78$ fully as it leaves a nonzero remainder of $6$. Thus, $9$ and $8$ are not factors of $78$.

Note that in Step-8 and Step-9, we get the same pair of quotients and remainders i.e., $(8,9)$ and the remainder is also the same i.e., $6$. This means that all the factors of $78$ have been obtained. So, we must stop the process.

Hence, the factors of $78$ are: $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$.

Prime Factorisation of 78

A prime number is a positive integer $P$ that has only two factors (not considering the negative factors here). For example, $2$, $3$, $5$ etc.

One of the most useful methods of finding the factors of an integer is prime factorisation. In this method, we factorise an integer only into its prime factors. Let us find the prime factorisation of 78 This can be obtained by the following few steps:

1. In the first step, we take the smallest prime number $2$, and check whether it divides $78$ or not. Obviously, as $78$ is an even number, $2$ divides $78$ completely as it does not leave any non-zero remainder while dividing $78$. Therefore, $2$ is a prime factor of $78$ and 78/2 = 39.

2. Next, we take the quotient $39$ obtained in the first step and check whether $2$ divides $39$ or not. Clearly, $2$ does not divide $39$ because $39$ is an odd integer.

3. Next, we proceed to the next prime number i.e., $3$, and check whether it divides $39$ or not. As the sum of the digits of $39$ is $3 + 9 = 12$ which is divisible by $3$, so, $3$ divides $39$. Also, $39\div 3=13$. Therefore, $3$ is a prime factor of $78$.

4. Now, the quotient $13$ obtained in the third step is a prime number. So, it is not divisible by any number other than $1$ and $13$ itself. Also, $13\div 13=1$. Hence, $13$ is a prime factor of $78$.

As we have got $1$ as a quotient at the end, we cannot proceed further because $1$ is not a multiple of any prime numbers.

In brief, we perform the following in the above four steps:

$78\div 2 =39$

$39\div 3 =13$

$13\div 13 =1$

Therefore, the only prime factors of $78$ are $2$, $3$, and $13$. Moreover, the prime factorisation of $78$ is $78=2\times 3\times 13$. The prime factors of $78$ can be represented by the following upside-down division method:

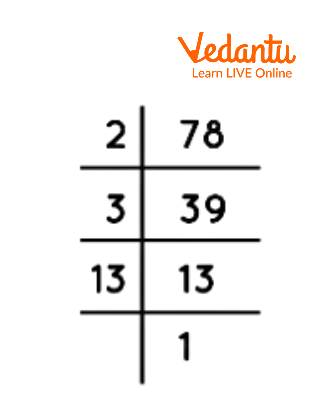
Prime Factorisation of 78

Now, we can find all the factors of $78$ by prime factorisation as follows:

• First, write all the prime factors as many times as they occurred: $2,\text{ }3,\text{ }13$. Each of them occurs only once in the prime factorisation of $78$.

• Now, multiply them with each other and get $2\times 3=6$, $2\times 13=26$, $\text{3}\times 13=39$, $2\times 3\times 13=78$.

• Also, $1$ is a factor.

• Now, list all the factors. Hence, all the factors of $78$ are: $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$.

Factor Tree of $78$

In a specific diagram known as a factor tree, we identify the factors of a number.

The set of prime numbers that when multiplied together give the original number 78 is called the factor tree of 78.

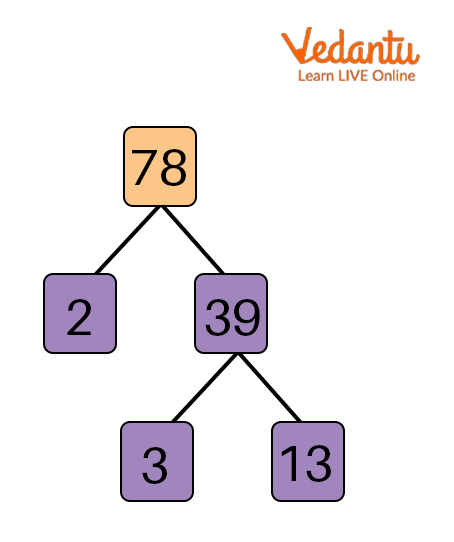
Factor Tree of 78

Factors of 78 in Pairs

A pair factors of $78$ will be a pair of factors $\left( {{f}_{1}},{{f}_{2}} \right)$ of $78$ whose product ${{f}_{1}}\times {{f}_{2}}$ equals to $78$.

We have, from the factorisation of $78$,

$78=1\times 78$

$78=2\times 39$

$78=3\times 26$

$78=6\times 13$

Hence, by definition, the pair factors of $78$ are: $(1,78)$, $(2,39)$, $(3,26)$ and $(6,13)$.

Interesting Facts

• The only factor of $78$ that is a perfect square is $1$.

• The smallest multiple of $78$ which is a perfect square is $78\times 78=6084$.

• The sum of all the factors of $78$ is $168$.

• There are no factors of $N$ in between $\dfrac{N}{2}$ and $N$?

Solved Examples

Example 1: What are the common factors of 27 and 78?

Solution: The factors of $27$ are $1,\text{ }3,\text{ }9,\text{ }27$ whereas the factors of $78$ are $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$.

Hence, the factors common to both $27$ and $78$ are $1$ and $3$.

Example 2: What is the average of factors of 78?

Solution: The number $78$ has a total of $8$ factors and those are $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$.

Now, the average of the factors will be the sum of all the factors divided by the number of these factors.

The sum of all the factors of $78$ is $s=1+2+3+6+13+26+39+78=168$ and the total number of these factors is $n=8$.

Therefore, the average of the factors of $78$ will be $a=\dfrac{168}{8}=21$.

Example 3: Ravi has 78 flower plants. He wants to plant them in 6 rows such that each row contains an equal number of plants. How many plants should he plant in each row?

Solution: Total number of flower plants$=78$.

Ravi wants to plant them in $6$ rows such that each row contains an equal number of plants. So, the number of plants he should plant in each row will be $78\div 6=13$.

Practice Questions

1. Find those factors of $78$ which are even numbers.

2. Find H.C.F. of $117$ and $78$.

3. Is there any factor of $78$ which lies between $39$ and $78$? Justify your answer.

4. Find a factor of $78$ which is also a factor of $180$.

Answer

1. $2,\text{ }6,\text{ }26,\text{ }78$.

2. $39$.

3. No, because there does not exist any factor of a number of $N$ that lies in between $\dfrac{N}{2}$ and $N$.

4. $2/3/6$.

Conclusion

The factors of $78$ can be obtained by several methods such as Division Method, Prime Factorisation Method, etc. It has a total of $8$ factors: $1,\text{ }2,\text{ }3,\text{ }6,\text{ }13,\text{ }26,\text{ }39,\text{ }78$ among them, there are only three prime factors that are $2$, $3$ and $13$. Prime factorisation of $78$ is $78=2\times 3\times 13$.