




How to Use the Expansion Method to Solve Multiplication Problems
Let's start with an example: suppose you go to the market and buy 62 apples, and 1 apple costs 7 rupees. You have to calculate the rupees spent to buy 62 apples. Here, we can expand the number into two parts $60+2$. Now multiply $60 \times 7=420$ and $2 \times 7=14$, and the total rupees would be 434. So it's quite easy to multiply using the expansion method. In this article, we will learn about the expanded form multiplication and box method of multiplication. We will also solve some practice questions.
What do You Mean by Expanded Form Multiplication?
The expanded form of multiplication is useful for splitting the higher-order digits and representing them in the form of units, 10s, 100s, and 1000s. Expanded forms help you better understand and read the top digits correctly. When solving multiplication problems using expanded form, you give each digit a value based on its position within the number.
Writing Numbers in Expanded Form
A number expansion is the separation of numbers by their place values. This is an intermediate step that helps you understand how to read numbers. The expanded form is useful for knowing the number of digits in each number. Also, there are three different ways to write numbers in expanded form. The number 4537 is expanded in one form as $4537=4000+500+30+7$, in a second form as
$4531=4 \times 1000+5 \times 100+3 \times 10+7 \times$ 1.
And in the third form can be written as
$4537=4 \times \operatorname{thousand}(1000)+5 \times \operatorname{Hundred}(100)+3 \times \operatorname{ten}(10)+7 \times$ one (1).
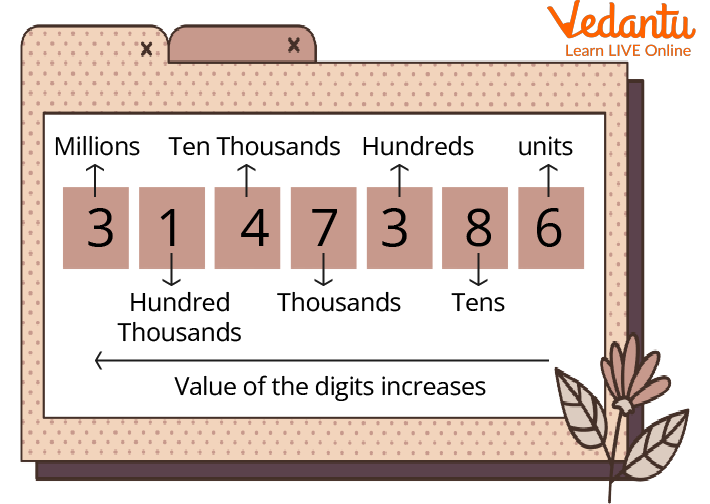
Placing Value in the Place Value Chart
Expansion Method Multiplication
In the Expansion Method of Multiplication, we generally expand the number using expanded form into place value then we multiply the units and add them together.
For example, Multiply by expanding the bigger number, $25 \times 5$
We separate the number into two unit
20 (in Tens place value) and 5 (in one place value)
$20 \times 5=100$
$5 \times 5=25$
$100+25$ (Now add the number)
= 125
Thus the multiplication of 25 and 5 using an expanded form is 125.
Box Method of Multiplication
The box method is another way to multiply two-digit and three-digit numbers. Instead of stacking numbers and remembering placeholders, the box method expands numbers and uses addition. The box method reduces multiplication to the basic ability of addition, without having to remember all the tedious rules that come with traditional multiplication.
Box Method Formula and its Use
To use the box method for multiplication, we need to follow a few steps.
Write both numbers in expanded form
Draw a box based on the number of digits in each number
Multiply each row and column of the box by the corresponding number
Add the numbers in the box to get the final value.
The first step in using the box multiplication method is to write each number in expanded form. Writing numbers in expanded form means writing each number separated by various digits 1, 10, 100, etc. added together.
The image below shows exactly what this box will look like when fully set up. Multiply to fill individual boxes and then take the sum to obtain the corresponding product, i.e. 3440 + 688 = 4128.
Thus, the multiplication of 12 and 344 gives 4128.
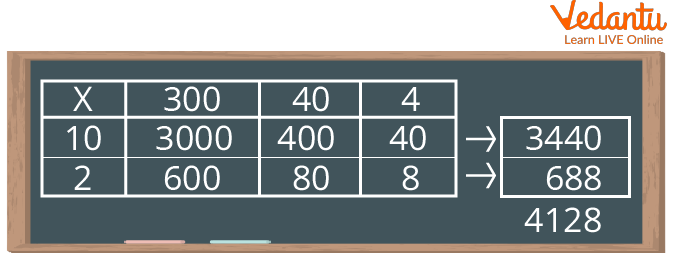
Box Method Calculation
Solved Examples
Q 1. Multiply by expanding the bigger number, $902 \times 7$.
Ans: We separate the number into two units
900 (in Hundred place value), 00 (in tens place value), and 2 (in one place value)
Now, multiplying $900 \times 7=6300$
$00 \times 7=00$
and $2 \times 7=14$
$6300+00+14$ (Now add the number)
= 6314
Thus the multiplication of 902 and 7 using an expanded form is 6314.
Q 2. Multiply by expanding the bigger number using the box method for 34 and 5344.
Ans: Set the box to multiply 34 and 5344. Looking at the two numbers above, we can see that 34 has 2 digits and 5344 has 4 digits. You will need to set up $2 \times 4$ boxes. The image below shows exactly what this box will look like when fully set up. Multiply to fill individual boxes and then take their sum to obtain the multiplication of two numbers, i.e. $160320+21376=181696$
Thus, the multiplication of 34 and 5344 gives 181696.
Practice Questions
A. Using Expansion Method:
Q 1.954 90.
Ans: 85860
Q 2. $769 \times 2$.
Ans: 1524
B. Using Box Method of Multiplication:
Q 1.5054 90.
Ans: 454860
Q 2. $769 \times 20$.
Ans: 15380
Summary
In this article, we have learned about how to use the expanded form multiplication & expansion method to expand the biggest digit and put them into place with values of ones, tens, hundreds, and so on. We learned how to multiply them and take their sum to get the result of multiplication. We also learn about the box method of multiplication. It solves multiplication problems using a box, which is drawn taking into mind the number of digits. Some examples and practice problems are also given for clarity of concepts.
FAQs on Expansion Method of Multiplication Made Easy
1. What is the expansion method of multiplication?
The expansion method of multiplication, also known as the expanded form method, is a technique where numbers are broken down into their place value components before being multiplied. For example, the number 47 is expanded to 40 + 7. Each part is then multiplied separately, and the results, called partial products, are added together to get the final answer.
2. How do you multiply using the expansion method? Explain with an example.
To multiply using the expansion method, you follow these steps. Let's take the example of 35 × 5:
- Step 1: Write the larger number in its expanded form. Here, 35 becomes 30 + 5.
- Step 2: Multiply each part of the expanded number by the other number. So, we calculate (30 × 5) and (5 × 5).
- Step 3: Find the value of these partial products. 30 × 5 = 150, and 5 × 5 = 25.
- Step 4: Add the partial products together to get the final result. 150 + 25 = 175.
Therefore, 35 × 5 = 175.
3. Why is learning the expansion method important before using the standard multiplication algorithm?
Learning the expansion method is a crucial step in the NCERT syllabus because it builds a strong conceptual understanding of place value. It shows a student *why* multiplication works the way it does by making each step visible. This prevents rote memorisation and helps students grasp that they are multiplying tens and ones, not just single digits. This foundation makes it much easier to understand the more compact, standard algorithm later on.
4. What is the main difference between the expansion method and the standard (short) multiplication method?
The main difference lies in how they display the calculation process. The expansion method breaks down the problem and shows all the partial products explicitly. In contrast, the standard method is a shortcut that combines these steps, often involving 'carrying over' numbers, which hides the full place value calculations. The expansion method prioritises understanding, while the standard method prioritises speed.
5. How does the expansion method of multiplication relate to the distributive property of maths?
The expansion method is a perfect practical example of the distributive property of multiplication over addition. This property states that a × (b + c) = (a × b) + (a × c). When we solve 5 × 35, we first expand 35 into (30 + 5). The calculation 5 × (30 + 5) becomes (5 × 30) + (5 × 5), which is exactly what the distributive property defines. This method helps students intuitively understand this fundamental mathematical law.
6. Can the expansion method be used for multiplying larger numbers, like a 3-digit number by a 2-digit number?
Yes, the expansion method works perfectly for larger numbers, although it requires more steps. For example, to multiply 123 × 24, you would expand both numbers:
- 123 becomes 100 + 20 + 3.
- 24 becomes 20 + 4.
You would then multiply each part of the first number by each part of the second (e.g., 100×20, 100×4, 20×20, 20×4, etc.) and add all the partial products. It effectively demonstrates how multiplication scales up.
7. What is a real-world example of using the expansion method for mental maths?
A common real-world example is calculating costs quickly without a calculator. Imagine you want to buy 4 notebooks that cost ₹32 each. Instead of struggling with 32 x 4, you can use the expansion method in your head. You think of 32 as 30 + 2. Then you calculate:
- 4 × 30 = 120
- 4 × 2 = 8
Then, you simply add them: 120 + 8 = 128. This makes it easy to figure out that the total cost is ₹128.

















