What Are Factors With Solved Examples and Step by Step Methods
There is a number which divides with another number without leaving any reminder. We can find factors from two ways: multiplication and division. A number can be multiplied with another number to give a product so these numbers are called factors.
Examples of Factors:
Let me have 10 mangoes and we have to divide that 10 mangoes between 10 people so that each person has an equal number of mangoes. So ,here \[1 \times 10 = 10\] from this example we can conclude that one is a factor of 10. Now we decide to divide 10 mangoes between five people so that each person has an equal number of mangoes so we can give two mangoes to every person. Now \[5 \times 2 = 10\]. Now again we decide to share 10 mangoes between two people. Each person has an equal number of members so we can give five mangoes to every person now \[2 \times 5 = 10\]. So the factors of 10 are 1,2,5,10. So from this example we can conclude that when a number is divided by its factor then the remainder becomes zero.
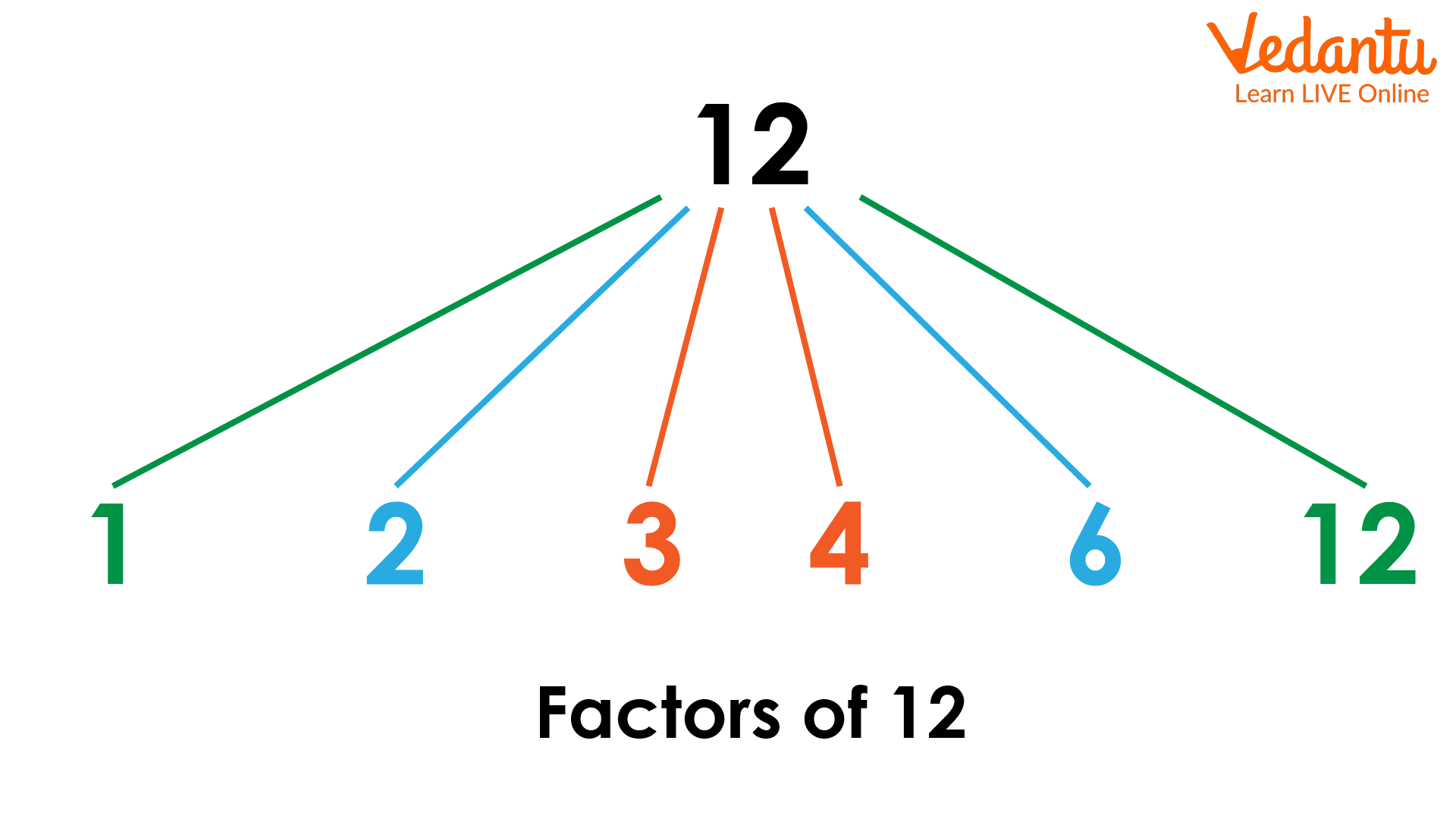
Factors of 12
Common Factors:
Common factor is a number which is a factor of two or more numbers that implies two numbers that can be divided with the same number without leaving any reminder. 1 is the common factor to all the numbers. To find a common factor of two or more Numbers, firstly we have to write down factors of every number independently and after that we have to check which factors are common in both the numbers, the factors which are common in all the numbers are common factors.
Example: found out the common factors of 12, 18, 26, 30
Factors of 12 –1,2,3,4,6,12
Factors of 18–1,2,3,6,9,18
Factors of 26 –1,2,13,26
Factors of 30–1,2,3,5,6,10,15,30
Common factors of 12, 18, 26, 30 are 1 and 2.
HCF:
HCF is called the highest common factor as its name suggests it is the highest common divisor of two or more numbers. Is also known as GCF, which is the greatest common factor. Now let’s discuss how to find HCF, so to find HCF of two or more number firstly we have to find factors of numbers separately and after that we have to find which factors are common after finding common factors we have to find which factories largest to all the numbers so the largest factor is called HCF.
Now let’s understand HCF with the help of an example. Let’s take two numbers 58 0 and 78 and find HCF.
Factors of 58 –1,2,29,58
Factors of 78 –1,2,3,6,13,26,39,78
Common factor of 58 and 78 –1,2
GCF of 58 and 78 is 2.
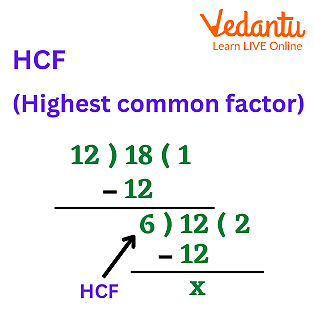
HCF
LCM:
It is the smallest number that is Multiple of two or more numbers. Let’s discuss LCM with the help of examples, take two numbers 3 and 5
Multiples of 3 are 3, 6, 9, 12, 15,…..
Multiples of 5 are 5,10,15,…..
Common numbers are 15,30,45,…..
The lease from all the common multiples of 3 and 5 is 15. Hence 15 is LCM of 3 and 5
LCM
Prime Factorisation:
When products of prime numbers are expressed as non prime numbers or composite numbers then this process is called prime factorisation. Now first discuss what prime numbers are: prime numbers are those numbers that only have two factors 1 and the number itself. Some prime numbers are 2,3,5,7,11,13,..so on. We can find prime factors with the help of tree method or division method. Let’s discuss some examples of prime factorisation
Prime factors of 12 –2x2x3
Prime factors of 36 –2x2x3x3
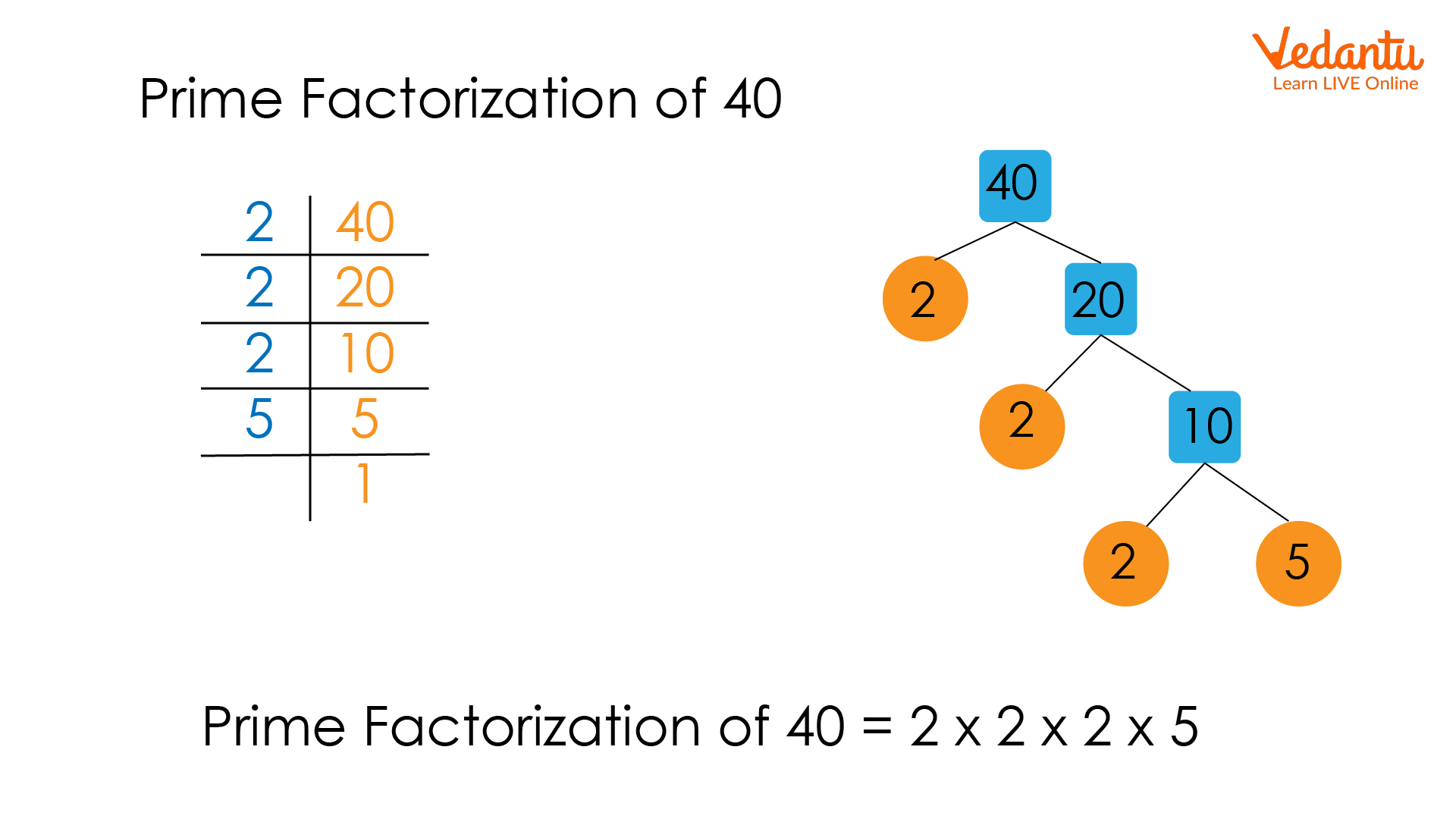
Prime Factorization
Solved Examples:
Q1. Find GCF of 28 and 34.
Solution: Factors of 28 – 1, 2, 4, 7, 14
Factors of 34–1, 2, 17, 34
Common factors of 28 and 34 –1,2
GCF of 28 and 34–2.
Q2. Find the LCM of 15 and 18
Solution:Multiples of 15 –15, 30, 45, 60, 75, 90, 105,…
Multiples of 18 –18, 36, 54, 72, 90,…..
So LCM of 15 and 18 is 90
Q3. Find the common factor 60 and 70
Solution:Factors of 60– 1,2,3,4,5,6,10,12,15,20,30,60
Factors of 70–1,2,5,7,10,35,70
Common factors of 60 and 70 are1,2,5,10
Conclusion:
In this article we learned about factors with the help of examples. We also learned about HCF, LCM , prime factorisation, and common factors. We also learn about how does Numbers are interrelated to each other. Like without finding common factors we cannot find it safe for LCM.
FAQs on Examples of Factors in Mathematics Explained Clearly
1. What are factors in maths?
A factor of a number is a whole number that divides it exactly without leaving a remainder. In other words, if a number can be multiplied by another whole number to get a given number, both are factors. For example, factors of 12 are:
- 1 × 12
- 2 × 6
- 3 × 4
2. What are some examples of factors of 24?
The factors of 24 are the numbers that divide 24 exactly with no remainder. To find them, check multiplication pairs:
- 1 × 24
- 2 × 12
- 3 × 8
- 4 × 6
3. How do you find the factors of a number?
To find the factors of a number, divide it by whole numbers starting from 1 up to the number itself and check which divisions give no remainder. Follow these steps:
- Start with 1 and check divisibility.
- Continue testing numbers up to half of the given number.
- List all numbers that divide exactly.
4. What are the factors of 36?
The factors of 36 are all whole numbers that divide 36 without leaving a remainder. Using multiplication pairs:
- 1 × 36
- 2 × 18
- 3 × 12
- 4 × 9
- 6 × 6
5. What is the difference between factors and multiples?
The main difference is that factors divide a number exactly, while multiples are obtained by multiplying a number by whole numbers. For example, for the number 5:
- Factors of 5: 1 and 5
- Multiples of 5: 5, 10, 15, 20, …
6. What are common factors? Can you give an example?
A common factor is a number that divides two or more numbers exactly. For example, consider 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
7. What are prime factors? Give an example.
Prime factors are prime numbers that multiply together to give a composite number. For example, to find the prime factors of 20:
- 20 = 2 × 10
- 10 = 2 × 5
8. What are the factors of a prime number?
A prime number has exactly two factors: 1 and the number itself. For example, 13 is a prime number because its only factors are 1 and 13. No other whole number divides 13 exactly.
9. What are the factors of 100?
The factors of 100 are all numbers that divide 100 without a remainder. Using multiplication pairs:
- 1 × 100
- 2 × 50
- 4 × 25
- 5 × 20
- 10 × 10
10. Why are factors important in maths?
Factors are important because they help in finding the HCF (Highest Common Factor), simplifying fractions, and performing prime factorization. For example:
- To simplify 12/18, use common factors.
- HCF of 12 and 18 is 6.
- Prime factors help in solving LCM and algebra problems.
