Division by Grouping Explained for Students

As we all know, there are four basic arithmetics in mathematics: Addition, Subtraction, Multiplication, and Division. So, in this chapter, we are going to learn about division. How numbers can be divided by the grouping method, and how it differs from equal sharing. Division by grouping is a strategy used to introduce the basic concept of division. It involves collecting an amount into equal groups and counting how many groups can be made. It can also be defined as splitting large groups into smaller groups so that every group will have an equal number of items. It is an operation used for equal sharing and equal grouping in mathematics.

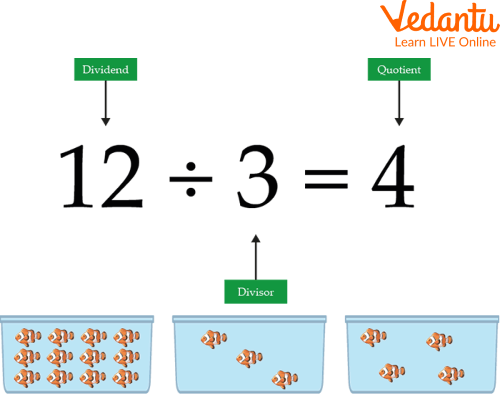
An Example of Division

What is Grouping?

Grouping can refer to a set of people, things, or numbers with something in common.

There are four types of grouping:

• Grouping by Number: Make groups of required numbers as illustrated, like groups of 5, 10, 2, and 4.

• Grouping by Type: Going by the definition of grouping, similar items need to be arranged together. In the given an example, the source has all the alphabet mixed up

Our task is to put ‘A’s, ‘B’s, and ‘C’ s, as shown in the results.

So the outcome of this exercise is that we have separate groups of A, B, and C.

• Grouping by Division: Grouping by division is splitting into equal parts or groups.

It is the result of “ fair sharing”.

• Grouping by Multiplication: Multiplication is the repeated addition of a group with equal items. Like in this example, its repeated addition of a group with 3 apples added 3 repeated times which results in a total of 9 apples.

So in this topic we are going to learn about grouping by division in detail:

Division by Grouping

The division is split into equal parts or groups. It is the result of “fair sharing”. Here is the division of $12 \div 3$. We begin with the number being divided, which is 12. We have 12 circles.

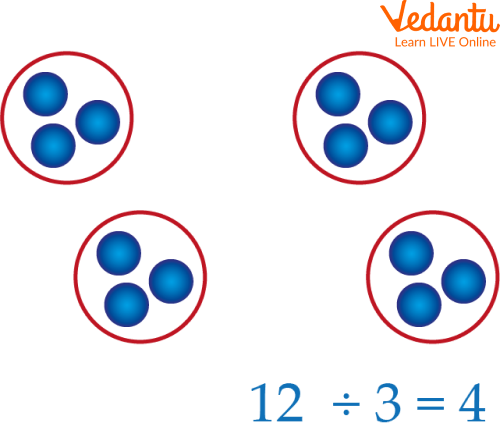
An example of division by grouping.

We are dividing 12 by 3 because there is 3 after the division sign in $12 \div 3$. The answer to the division tells us how many times 3 goes into 12. We can also discuss this as “How many groups of 3 can be formed from 6?” We can gather the 12 circles into groups of 3 as shown in the image mentioned above. We have 4 circled groups, which means that 4 groups can be made of 3 circles. Our answer to the division is 4.

How to Divide with Equal Groups?

There are following steps need to be followed to divide into equal groups:

1. Draw the same number of dots or circles as the number being divided.

2. Count the dots or circles until there is a number for division.

3. Draw an outer circle around these dots or circles.

4. Repeat steps 2 & 3 until all of the dots or circles are grouped.

5. Count the number of groups there.

6. The number of groups is the answer to the division.

Equal Sharing Division

Difference Between Equal Grouping and Equal Sharing

There are two means of teaching division: equal sharing and equal grouping. Sharing is probably the most common princess of division. In the problems of equal sharing, we begin with the number of objects needed to be shared. Our main aim is to find out how many objects each (equal) group can receive.

For example, let’s say we have 15 chocolates and want to share them with 5 friends. How many chocolates does everyone get?

$15 \div 5 = 3.$

Sharing can be the most familiar approach to division, but it is not the only way. In an equal group problem, we know that the number of objects each group should receive, as well as the total number of objects, can be distributed. The objective is to determine how many equal groups can be created.

Now we want to make boxes of chocolates for our friends. Each box has 3 chocolates, and we have 15 chocolates. How many boxes can we make?

$15 \div 3 = 5.$

Solved Examples

Q 1. Share eight strawberries between four children.

Strawberries between four children.

Ans: Let us distribute strawberries equally to all four children one by one.

Strawberries between four children.

After distributing equally among four children, four strawberries were left. They can be further distributed among four children.

Strawberries between four children.

Now, there are no more strawberries left in the box. Each child got 2 strawberries. So, the division is an operation of repeated subtraction of the same number.

8 – 4 = 4

4 – 4 = 0

Here, we subtracted 4 repeatedly 2 times until we reached 0.

Hence, 8 strawberries ÷ 4 children = 2 strawberries for each child.

Q 2. Shirley and John had 12 flowers to share among themselves. How many flowers do they each get if it is shared fairly?

12 flowers for 2 person

Ans:

$12 \div 2 = 6$.

6 flowers for each

So, both of them get 6 flowers each.

Practice Questions

Here we have provided worksheets on division by grouping. Practising these questions will help you get a better understanding of the concept.

Q 1. A farmer shares 28 sugarcanes with his 4 children. How many sugarcanes his every child gets?

Ans: 7

Q 2. If you are given 8 bananas, and you have to divide them in 2 groups? How many bananas will each group receive?

Ans: 4

Q 3. How will you distribute 12 chocolates among 6 kids?

Ans: 2 chocolates to each kid.

Summary

In this chapter, we have learned that for a better understanding of division by a group, it is necessary to introduce division as a physical model. The method of division by grouping helps to understand the meaning behind division. Division by grouping is not a method suggested for the long term but is very useful for children who are still learning timetables and facts of division. We also understood the difference between equal grouping and equal sharing division. It is very important to know about the facts regarding division quickly so that less effort and time is spent in order to learn about the same.