How to Apply the Division Algorithm: Formula, Proof & Solved Examples
The division algorithm formula is a systematic way of verifying the long division of two numbers or two polynomials. The division formula is a less tedious way of verifying the long division method. Let us learn more about the division algorithm.
What is the Division algorithm?
Before we dive into using the division algorithm with polynomials we first need to understand what a division algorithm is. Euclid gave the division algorithm. You must be familiar with dividing two numbers. [say]
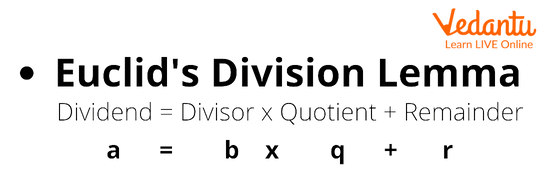
Division algorithm
Division Algorithm Formula for Numbers
The division algorithm formula in numbers states that when a positive number a is divided by another positive number b, we get a unique quotient q and a unique remainder r. Here we say that q and r are positive integers and r is greater than or equal to 0 and less than b.
Division Algorithm in Numbers
Properties of Division Algorithm
A positive number can only be divided by a smaller number.
If the divisor is not a factor of the dividend, then a non-zero remainder will be left behind.
There is a unique pair of quotients and remainder.
Steps to do Division of Two Numbers
Always remember that the divisor is always smaller than the dividend
First, notice the first digit from the left of the dividend. if the divisor is less than the first digit then take the 2nd digit as well, and put a 0 in the quotient as many times as you find the dividend less than the divisor and keep repeating this process till you get the dividend greater than or equal to the divisor.
now write the largest multiple of the divisor that is less than the dividend and write the quotient.
Subtract the multiple from the dividend and write down the next digit of the original dividend.
Repeat steps 2, 3, and 4. Till you get a remainder smaller than the divisor.
Solved Examples
1. Divide the numbers 6 and 250.
Ans. Here the divisor is 6 and the dividend is 250.
Step1. First, we see that 6 cannot divide 2 so we write 0 and include the 5 in our dividend.
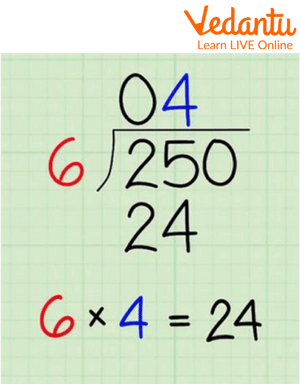
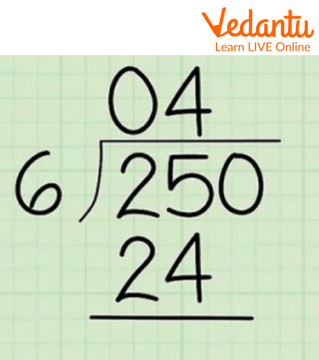
Division Algorithm example
Step2. Now we see that 25 is greater than 6 so we start the division process. We will write the largest multiple of 6 which is less than 25. We have 6 x 4 = 24. So 4 will be our quotient and 24 will now be subtracted from the dividend.
Division Algorithm example
Step3. This gives 1 as the remainder. Now we use the 0 left in the dividend. Now our new dividend is 10.
Division Algorithm example
Step4. Now we can see 6 x 1 = 6. So 1 will be our quotient and we will have a remainder of 10 - 6 = 4. As we can see 4 is less than 6, and we are finished with the problem. Hence, our quotient is 41 and the remainder is 4 and the division algorithm formula will be, 250 = ( 6 x 41 ) + 4.
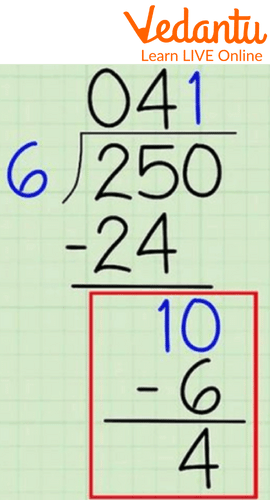
Division Algorithm example
2. Divide 813 by 9 and verify the result by the division algorithm.
Ans. We have a divisor as 9 and dividend as 813.
We first start with 9 and 8, we see that 8 is less than 9 so we use 1 as well. Now we see that 9 x 9 = 81. so 9 will be our quotient and we write down 81 under 81 and subtract it. We get 0 as the remainder now we use 3 from the original dividend. Now we see that 3 is less than 9 so we add 0 at the end of the quotient, so our quotient is 90, and we have a remainder of 3. Now we need to verify this, we have
813 = ( 9 x 90 ) + 3 from the division algorithm formula
813 = 810 + 3
813 = 813
Hence, verified.
Conclusion
A division algorithm is an essential tool for verifying and proving important facts in mathematics. We have learned how to use the division algorithm formula. We have learned some of its important properties and solved several examples.
FAQs on Division Algorithm Formula Explained for Students
1. What is the division algorithm formula?
The division algorithm formula provides a formal way to express the outcome of dividing two integers. It is stated as: Dividend = (Divisor × Quotient) + Remainder. This equation shows that any dividend can be expressed as a product of its divisor and quotient, plus any leftover remainder.
2. What are the four main components in the division algorithm?
The four main components of the division algorithm are:
Dividend: The number that is being divided.
Divisor: The number by which the dividend is divided.
Quotient: The whole number result of the division.
Remainder: The value left over after the division is complete.
3. Can you explain the division algorithm with a simple example?
Certainly. Let's divide 38 by 5. Here, the Dividend is 38 and the Divisor is 5. When we perform the division, we get a Quotient of 7 and a Remainder of 3. According to the division algorithm formula:
Dividend = (Divisor × Quotient) + Remainder
38 = (5 × 7) + 3
38 = 35 + 3
38 = 38.
This verifies that the division is correct.
4. What is the most important condition for the remainder in the division algorithm?
The most important condition for the remainder (r) is that it must be greater than or equal to zero and strictly less than the divisor (d). This is mathematically expressed as 0 ≤ r < d. This ensures that the quotient and remainder for any pair of integers are unique.
5. What is the importance of the division algorithm in mathematics?
The division algorithm is fundamentally important because it is the bedrock of number theory. Its primary application is in Euclid's algorithm, which is used to efficiently find the Highest Common Factor (HCF) of two integers. It also proves the existence and uniqueness of quotients and remainders, a concept crucial for modular arithmetic and abstract algebra.
6. Is the division algorithm the same as Euclid's division lemma?
While closely related, they are slightly different. Euclid's division lemma is the formal theorem that states for any two positive integers 'a' and 'b', there exist unique integers 'q' (quotient) and 'r' (remainder) such that a = bq + r, where 0 ≤ r < b. The division algorithm refers to the actual step-by-step procedure (like long division) used to find this 'q' and 'r'. The lemma guarantees that the algorithm will always work.
7. Does the division algorithm only apply to integers, or can it be used for polynomials too?
The division algorithm is not limited to integers; it has a crucial application for polynomials as well. For any two polynomials, p(x) (dividend) and g(x) (divisor), where g(x) is not the zero polynomial, there exist unique polynomials q(x) (quotient) and r(x) (remainder) such that: p(x) = g(x) ⋅ q(x) + r(x), where the degree of r(x) is less than the degree of g(x) or r(x) = 0.
8. What does it mean if the remainder is zero in the division algorithm?
If the remainder is zero after applying the division algorithm, it signifies that the dividend is perfectly divisible by the divisor. In other words, the divisor is a factor of the dividend. For example, when dividing 20 by 4, the remainder is 0, which confirms that 4 is a factor of 20.
