




What Is the Perimeter of a Cube? Definition, Formula, and Tips
This article provides information about the perimeter and surface area of a cube, including what they are and the formulas used to calculate them. The perimeter of a cube is simply the distance around the outside of it, while surface area is how much space it takes up. The formula for perimeter and surface area of a cube is 12a and 6$a^2$, where a represents the length of the cube.
So the perimeter is the length of the sides, and the surface area is how much it takes up. It could be helpful to know some formulas to help calculate these.
Surface Area of a Cube
The total area of all the cube's faces makes up the surface area of the object. We are aware that every face in a cube is equal, or that they all have the same area. By multiplying the area of one of its faces by six, we may determine its surface area.
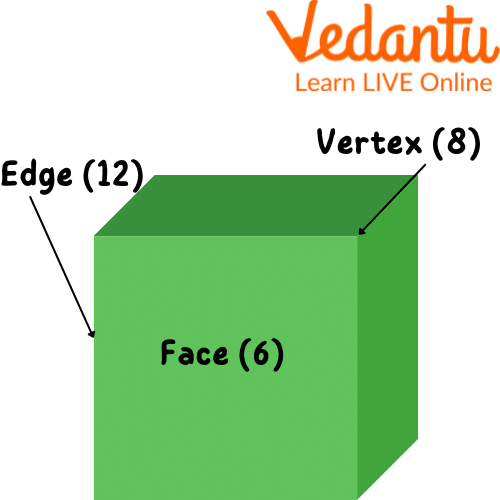
Shape of a Cube
Now let’s learn about cube area and perimeter formulas.
The total area of all the cube's faces makes up the surface area of the object. We must sum the areas of each of the cube's six faces in order to get its surface area because it has six faces.
We are aware that the cube contains a square figure on each face. As a result, the square of one side's length is equal to the area of each face of the cube. If an is used to represent one of the sides' lengths, we get the following:
Area of a cube face $=a^{2}$
If we add the six faces, we have:
$A_{s}=a^{2}+a^{2}+a^{2}+a^{2}+a^{2}+a^{2}$
$A_{s}=6 a^{2}$
where $A_{s}$ represents the surface area and $a$ represents the length of one side of the cube.
Cube Perimeter formula
Let’s discuss how to find the perimeter of a cube formula. The lengths of all the cube's sides, often referred to as its edges, add together to form the perimeter of a cube. There are a total of 12 edges in a cube.
The perimeter of one face of cube formula:
$p=4a$
Additionally, since a cube is a regular shape, all 12 of its edges must be the same length. Taking all of this into account, we can derive the cube perimeter formula shown below:
$p=12 a$
where $a$ is the length of one of the edges of the cube.
Now we have command over the cube area and perimeter formula. Let’s see some solved examples based on it.
Solved Examples
Q1. The perimeter of a cube is 36 cm. Find the surface area of the cube.
Perimeter of a cube = 12a (a = side length)
Ans: Given that 12a = 36
$a=\dfrac{36}{12}$
$=3 \mathrm{~cm}$
Surface Area $=6 (a^2) =6 \times (3^2)$
$=6 \times 9$
$=54 \mathrm{cm}^{2}$
Q2. Find the perimeter of a cube having edges of a length of 5m.
Ans: Put length $a=5$ in the perimeter formula:
$p=12 a$
$p=12(5)$
$p=60 \mathrm{~m}$
The perimeter is equal to $60 \mathrm{~m}$.
Q3. Find the length of the sides of a cube that has a perimeter of $120 \mathrm{~m}$.
Ans: To find the length of the sides or edges, we have to use $p=120$ and solve for $a$ :
$p=12 a$
$120=12 a$
$a=\dfrac{120}{12}$
$a=10 m$
The sides have a length of 10m.
Q4. What will be the surface area of a cube if it has sides of a length of 10m?
Ans: Put $a=10$ in the surface area formula
$A_{s}=6 a^{2}$
$A_{s}=6(10)^{2}$
$A_{s}=6(100)$
$A_{s}=600 m^{2}$
The surface area is $600 \mathrm{~m}^{2}$.
Q5. Find the side length of a cube if it has a surface area of $240 \mathrm{~m}^{2}$.
Ans: Put the surface area in the formula and solve
$A_{s}=6 a^{2}$
$240=6 a^{2}$
$\dfrac{240}{6}=a^{2}$
$40=a^{2}$
$a=6.32 m$
The length of the sides is $6.32 \mathrm{~m}$.
Practice Questions
Q1. What is the length of the sides of a cube that has a perimeter of 144m?
Ans: 12 $m$
Q2. If a cube has sides of length 4m, what is its surface area?
Ans: 96 $m^2$
Q3. If a cube has a surface area of 54m2, what is the length of its sides?
Ans: 3 $m$
Q4. If the perimeter of one face of a cube is 20cm, then its surface area is
Ans: 150 $cm^2$
Q5. Each edge in a cube is 5 cm. What is the surface area in square cm?
Ans: 150 $cm^2$
Summary
One of the most prevalent three-dimensional solid objects is the cube. The length of each side of a cube is its defining property. 6 faces, 12 edges, and 8 vertices make up a cube. Examples of these figures in everyday life include the Rubik's cube and a conventional 6-sided dice. We discussed in the article the formula of perimeter of the cube as well as area.
When we wish to measure a two-dimensional quantity in the cube, the surface area is a measurement that might be helpful. The perimeter of a cube is equal to the total of its individual sides, commonly known as the cube's edges, much like the perimeter of a square is equal to the sum of its side lengths.

Real-life Examples of a Cube
FAQs on Cube Perimeter Formula Explained: Steps & Examples
1. How do you find the perimeter of a cube?
To find the perimeter of a cube, it’s important to clarify that a cube is a three-dimensional solid. Typically, cubes are described in terms of their edge length (s). If you want the total length of all the edges combined (sometimes referred to as the cube's 'perimeter'), use the formula:
$$ \text{Total Perimeter} = 12 \times s $$
where s is the length of one edge. This is because a cube has 12 edges of equal length. At Vedantu, detailed lessons and examples help you practice and understand these calculations thoroughly.
2. What is the area of a cube?
The surface area of a cube is calculated by finding the area of one face and multiplying by the total number of faces. Since each face is a square, and a cube has 6 faces:
$$ \text{Surface Area} = 6 s^2 $$
Here, s represents the length of one side of the cube. With Vedantu’s mathematics resources, students can explore surface area concepts through interactive examples and expert guidance.
3. Which is the formula for perimeter?
The formula for perimeter varies with the shape:
- Square: $4 \times s$
- Rectangle: $2(l + w)$, where l is the length and w is the width
- Cube (sum of all edges): $12 \times s$
4. What is the perimeter of a cubic rectangle?
A 'cubic rectangle' typically refers to a rectangular cuboid (a box-shaped solid). To find the total edge length (perimeter) for a cuboid with dimensions length (l), width (w), and height (h), use:
$$ \text{Total Edge Length} = 4 \times (l + w + h) $$
This formula sums the edges from all three dimensions. Vedantu’s subject experts help students master formulas and understand geometric measurements in depth.
5. What is the difference between the perimeter and surface area of a cube?
Perimeter (or, more accurately for a cube, the total edge length) measures the sum of all edge lengths of the cube ($12 \times s$), while surface area measures the total area covered by the cube’s six faces ($6s^2$). These concepts help distinguish between measuring length and area, an important topic in Vedantu’s mathematics curriculum.
6. How do you derive the formula for the perimeter of a cube?
A cube has 12 edges, each of equal length (s). To get the perimeter (total edge length), simply multiply the number of edges by the length of one edge:
$$ \text{Total Perimeter of Cube} = 12 \times s $$
Vedantu provides step-by-step derivations and interactive problem-solving to help learners easily grasp such geometric formulas.
7. Can the perimeter formula for a cube be used for other 3D shapes?
The cube perimeter formula applies only to cubes where all edges are equal. For other 3D shapes, such as cuboids, you must adjust the formula based on their dimensions. For a cuboid with edge lengths l, w, and h:
$$ \text{Total Edge Length} = 4(l + w + h) $$
Vedantu’s expert faculty helps students learn the correct formulas for a variety of geometric solids.
8. Why is understanding cube perimeter important in mathematics?
Knowing how to calculate the perimeter (total edge length) of a cube is crucial in many mathematical and real-life applications, such as solving geometry problems, constructing models, and calculating required materials. Vedantu’s teaching approach emphasizes applying these concepts in both academic and practical scenarios.
9. How can Vedantu help students master cube perimeter and related formulas?
Vedantu offers personalized online tutoring, interactive lessons, and a wide range of practice problems specifically focused on cube perimeter formulas and other geometry concepts. Students receive step-by-step guidance and can clarify doubts in real-time, helping them build a strong foundation in mathematics.
10. What real-life problems can be solved using the cube perimeter formula?
The cube perimeter formula is useful in scenarios like:
- Calculating the amount of edging or framing needed for a cube-shaped structure
- Determining material costs for wrapping or constructing objects
- Designing packaging and storage solutions

















